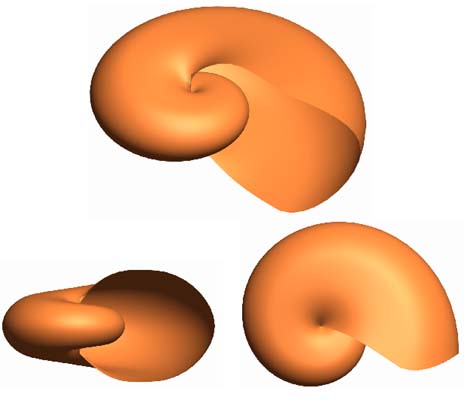Spiral patterns in shells & horns

Where we use a mathematical approach to model the shape of shells and horns of various kinds, with a special emphasis on the Nautilus.

Modeling shell and horn geometry

In this section, we introduce the mathematical concepts needed to model a great variety of seashells and horns.

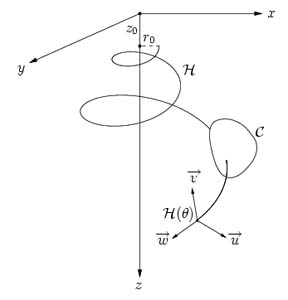
The logarithmic helico-spiral


Figure 3.1: Logarithmic helico-spiral and its "shadows".
As explained in the opening chapter, the pattern that shells exhibit are governed by logarithmic spirals of various kinds. For the Nautilus shell, the spiral lies in a plane P dividing the shell into two symmetric pieces. But for most other shells, the growth takes place along a logarithmic spiral which has been stretched along a coiling axis going through the pole and normal to P, axis we conveniently call the z-axis. This curve is the so-called logarithmic helico-spiral, which we denote H, and has the following parametric representation in cylindrical coordinates:

H= H(q) = ì
ï
í
ï
î
x(q) = r0 eqcota cosq= r(q) cosq
y(q) = r0 eqcota sinq= r(q) sinq
z(q) = z0 eqcotb
a, b Î   ù
û 		0,  p
2
 é
ë 		,  r0, z0 Î   R.
For physical reasons, we choose q Î  ]0, qmax[, where q = 0 at the apex of the shell, and q = qmax at its opening. In most shells, the angles a and b are equal, and thereby H moves on a right cone and its pole O is at the cone's apex. In fact, the angle j between the coiling axis and the line (OP), where P is moving on H, is given by tanj = r(q) / z(q) = r0 / z0. As can be seen, this angle is independent of q, and hence P will never leave the cone, whose opening angle is arctan (r0 / z0). If a and b are not equal, the proportion r(q) / z(q) depends on q, so the spiral does not move along a straight cone. As a consequence, the sought self-similarity properties are lost and therefore, this shape is not very common among shells. So in the following, it is assumed that a = b, i.e. that ř(q) = ž (q).

Generating curve and Frenet-Serret frame

When constructing the surface of a shell, we sweep a curve C along H, having the shape of the shell's aperture. This curve is called the generating curve and determines the profile of the shell. For example, in common shells such as the snail, this curve is approximately a half ellipse. However, more exotic variants have more complicated generating curves, such as the Thatcheria mirabilis shown on figure 3.3 (a).
Figure 3.3: Thatcheria mirabilis and Epitonium scalare.
The generating curve is defined in a local coordinate system uvw with origin moving along H. But there are various ways to orientate the coordinate axes. For instance, most shells exhibit orthoclinal growth, which means that the instantaneous tangent of H is normal to C, assumed to lie in the plane uv (cf. figure 3.4). This is particularly visible in the Epitonium scalare (figure 3.3 (b)), where the white ribs are not vertical but perpendicular to the spiral. Thus, it would be convenient to let the coordinate system uvw alone determine the orientation of C, so that we do not have to worry about this when defining C. In the orthoclinal growth case (illustrated on figure 3.4), we orient w along the unit tangent vector et of H. The vectors u and v are aligned with the unit principal normal vector en and the unit binormal vector eb of H, respectively. The triple {et,en, eb} is called the Frenet-Serret frame on H, and the components are defined by the relations
et =  H¢(q)
|| H¢(q) ||
 ,     en = et ×eb,     eb =  H¢(q) ×H" (q)
|| H¢(q) ×H" (q) ||
 ,    
where || ·|| denotes the usual Euclidean norm in R3. These formulas are well known in differential geometry, so we will not prove them right here (proofs can be found in [8]) and in [9]. One should note, however, that the Frenet-Serret frame is defined provided that H and H¢ are both regular. But this is obviously the case here, since H" never vanishes.
Figure 3.4: Construction of the shell with orthoclinal growth.
When we are not dealing with orthoclinal growth, which is the case when modeling the Nautilus, we do not need Frenet-Serret frames. The coordinate system uvw is simply translated and rotated so that its pole lies on H and that u and v are perpendicular and parallel to the z-axis, respectively. We will call this kind of growth vertical.
Now we need to scale C in order to get a surface whose aperture grows exponentially, in accordance with the exponential growth of the animal. Obviously, to preserve the self-similarity properties, C and H must grow at the same rate, which we call s. We put s = r(q) in order to express the growth rate qualitatively. Proper constants will be added in Raup's Model which we will encounter in the next section. So, the system uvw is defined, in the vertical case, as
u(q)
=
s ·(cosq, sinq, 0)
v(q)
=
s ·(0, 0, 1)
w(q)
=
u(q) ×v(q) = s2 (sinq, cosq, 0)
In the orthoclinal case, we have, of course, (u(q), v(q), w(q)) = s ·(et, en, eb).
The mathematical aspects being clarified, we are ready to bring the pieces together in Raup's Coiling Model.

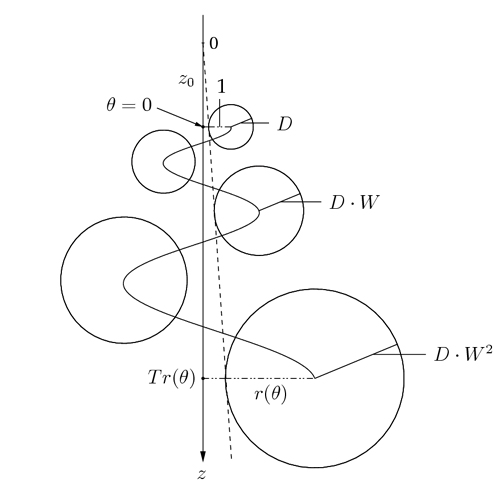
The Raup Coiling Model

The physical model

In 1962, Raup, [21] and [22], introduced a model of seashells consisting of four parameters whose meaning he expressed as follows:
A simple model of variation in the rate of growth in several dimensions accounts for variation in the form of gastropod shells. The model specifies the shape of the aperture, or generating curve, the axis of coiling, the size ratio (W) of successive generating curves, the distance (D) of the generating curve from the axis, and the proportion (T) of the height of one generating curve that is covered by the successive gyres.
This definition is very vague, but this has no importance; the important thing is namely the meaning of the four parameters, and the exact definition is up to us to formulate. In fact, when studying the morphology of shells and horns, one can imagine that a certain definition might be better suited for a special experimental device than another. So here is our definitions of the parameters W, D and T (illustrated on figure 3.5) 3:
Figure 3.5: Schematic section of a seashell with Raup's Coiling Model parameters shown.

To get an intuitive feeling of the meaning of Raup's Coiling Model parameters, try the Raup Coiling Model applet, where you can modify these in real-time on a three dimensional surface.

From a physical to a mathematical model

Our interpretation of Raup's model is well suited when we have sections of seashells, such as the one schematized on figure 3.5. However, when constructing the shell, we are interested in knowing the parameters needed in the mathematical model, such as the angle a or the initial radius r0, only implicitly contained in W, D and T. It is, however, straightforward to convert these parameters, as we will show now.
Let us consider a shell which does not exhibit orthoclinal growth, and whose generating curve C is a circle lying in the uv plane. This is the most simple setup, and it does not affect the following results when extended to more general cases. Now consider the projection of H onto the xy-plane, which is the logarithmic spiral given by the equation r = r0 eqcota (actually, this spiral is a special case of a helico-spiral with z0 = 0 in the parametrization ). The generating curve C is thereby projected onto a straight line segment aligned with the radius vector. Since the length of this segment is multiplied by W at each revolution, we get immediately, by theorem 2.3.4, that a = arccot ( ln(W) / 2p). Furthermore, we have chosen r0 = 1 for simplification, and this of course does not affect the model, since it is only a matter of scaling. As a consequence, D, being the radius of C at this point (q = 0), will most often be chosen in the interval ]0,1]. If D is chosen greater that 1, the generating curve will be on both sides of the z-axis, yielding odd shells that we have not encountered. T being the ratio between z(q) and r(q), we have in particular that z(0) / r(0) = z0 / r0 = z0 = T, so it is throught z0 that the stretching parameter T is expressed.

Shell generation

We are now ready to construct the seashell. So let
C= C(t) = (xC(t), yC(t), zC(t))
be a parametrization of C in uvw. Then the shell has the parametrization
S= S(q, t) = H(q) + D ·C(t) ·(u(q), v(q), w(q))T.
In a sketchy way, what happens here is that C is translated by the vector H(q), and thereby its center lies on H (by center we mean the origin of the coordinate system in which C is defined). Then C is scaled and rotated properly by means of the uvw system. Examples that illustrate the difference between the two growth types are shown on figure 3.6.
Figure 3.6: Seashell models with vertical (left) and orthoclinal (right) growth.

A more realistic generating curve

The above seashell models have been generated by a circle. However, this is a very simplistic model which is not realistic. In fact, the great diversity in shells is essentially provided by the different kinds of generating curves. This is clearly illustrated in the Thatcheria on figure 3.3. And there are many ways to represent shapes that can not be approximated by simple mathematical curves such as the circle. One of the ways is to use Bézier curves, which provide a very simple and intuitive representation of polynomial curves by means of control points. The use of Bézier curves is, nevertheless, not in the scope of this report. In fact, the problem is that, when using such curves, we move away from the initial driving idea, that is, that nature is built up around a few, simple and very precise elements. And the reason for these elements being present instead of others is clear. But when the generating curve is "arbitrary", and therefore best approximated using polynomial curves, we can not answer this question, "why?", anymore, and therefore it is of very limited interest that we study them. However, it yields some very beautiful pictures as well as interesting mathematical problems, and therefore we have tried, using these curves, to model shells which, concerning the generating curve, have no obvious reason to have the shape it has instead of any other!
Making the attempt to model seashells using Bézier curves was inspired by [7]. Other attemps have been made, for instance by Michael Cortie, as described in [10]. The idea is basically the same, except that Cortie includes parameters which control rotations of the uvw coordinate system, and thus, he is not limited to the vertical and orthoclinal cases - but they are more or less the only ones present in nature.

The Raup Coiling Model applied to various shells

Most shells and horns are simple enough to be modeled using Raup's Coiling Model, and in this section we apply it to construct several surfaces. Special emphasis has been put in the modeling of Nautilus, and other more or less comlicated figures are shown without further descriptions. They are simply the result of different Raup model parameter combinations and generating curves.

The Nautilus shell

The nautiloid family

Figure 3.7: The lituus (middle) found in various shapes: (top) the Lituite Lituus; (bottom) a violin neck.
The Nautilus pompidus (or simply Nautilus) is a mollusc belonging to the family of Nautiloids, which itself belongs to the wider family of marine molluscs called the Cephalopods. They emerged in the late Cambrian, approximately 500 million years ago, and are characterized by their chambered shell, where the outermost chamber is the one where the animal lives. The chambers are separated by walls (called septa) with a small funnel (the siphuncle), allowing the Nautiloid to inject a gas, essentially nitrogen, that will make it float.
Many different molluscs descended from this family, and among those, the Orthoceras, whose shell had a conical structure (cf. figure 2.11). According to the (unknown) author of the website [4], Most early nautiloids had straight conical shells.. However, these species did not survive; instead, new species developed by coiling their shell. An example of an "intermediate" species is the so-called Lituite Lituus, a "half-coiled up" cone (as shown of figure 3.7 (top)). The shell follows a curve which neither a straight line nor a logarithmic spiral, as in the two above mentioned extremes, but a lituus (figure 3.7 (middle)), whose polar equation is r = a / Ö{q}. This curve is also found extensively in architectural design, a known example being the neck of a violin.
The Lituite Lituus did not survive either. In fact, today there are only a few species left from the Nautiloid family (3 or 4, according to [14]) and they all belong to the Nautilus genus. This suggests somewhat that the Nautilus had better survival capabilities, which is quite understandable because of the more compact, and thereby less fragile, shape of the shell, compared to the conical or "semi-conical" ones of the Orthoceras and Lituite Lituus, respectively. It is also an interesting fact to know that the Nautilus migrates from depths of 500 meters to the water surface, by regularizing the gas in its chambers. This indicates the strength of its shell, tolerating extreme changes in pressure as well as temperature.
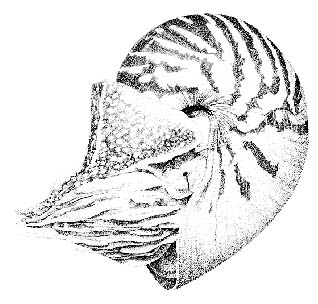Figure 3.8: A swimming Nautilus (illustration taken from http://waquarium.mic.hawaii.edu/MLP/root/html/MarineLife/Invertebrates/Molluscs/Nautilus.html).

Measurements on the Nautilus shell

The spiral of the Nautilus lies in a plane, and Therefore, T = 0. Furthermore, it seems reasonable to believe that the generating curve is tangent to the coiling axis, and thereby that D = 1. We have measured the constant by which the radius is incremented at each revolution, and found that in average, W = 2.93. We are not in possession of any precise measuring tool, so this result should not be taken seriously! However, the measurements on each shell are almost identical, which indicates that the actual Nautilus has found its very precise shell shape. On the website www.spirasolaris.com, John N. Harris points out that this growth constant is approximately equal to f7/3 @ 3.07353, f being the Golden Ratio that we will encounter in the next chapter. We do not know if this is a coincidence, but believe that the relation is a bit far-fetched, and has no interesting significance in our work.

Concerning the generating curve, it cannot be approximated by a simple mathematical curve, although one could argue that an ellipse does the job. We are not interested in that solution, especially because the curve is three dimensional, as depicted on the profile view of figure 3.9 (right). Therefore, to be as realistic as possible, we use the Bézier curves. We would like to emphasize on the fact that this choice is only made in order to model a beautiful and an as-realistic-as-possible shell surface. But, in the context of shapes generated by nature, we do not like the idea, since there is no explanatory value in an arbitrary curve which Bézier curves are. However, we can still suggest the reason for the apertures actual shape.
To that purpose, let us, conceptually, build up the Nautilus shell. As a starting point, we assume that the parameters W and T are known. In fact, that T = 0 is obvious because of the upstanding posture of the Nautilus. If T ¹ 0, the shell would not be symmetric, and thereby the animal would not be in its natural equilibrium position (cf. figure 3.8). The growth rate may also be assumed known, since it has no mathematical importance here, as long as it is greater than 1. Now imagine that the aperture of the shell is a circle which is tangent to the underlying whorl. Mathematically, this would be a perfect model expressing the same kind of growth as the Nautilus', that is, along a logarithmic spiral lying in a plane P. Such a "mathematical Nautilus" is shown on figure 3.10 (a). Now let us analyse a cross section of the shell generated by a plane perpendicular to P going through the pole of the spiral (figure 3.10 (b)). Clearly, this setup is not very well suited for several reasons: the innermost whorls of the shell are exposed to the surrounding environment; the structure is unstable because there is only one contact point between two neighboring whorl circles. A much more robust setup would be to imbricate the whorls, as depicted on figure 3.10 (c) and illustrated with the Ammonite of figure 3.10 (d). But proceeding to the extreme, why not let one whorl cover all the other ones? This is what we think the Nautilus has done when developing from the primitve Orthoceras to its actual shape, but we haven't got any confirmation of this. Another advantage of this configuration is that it permits the animal inside to adhere better to the shell because of the "bump" created by the underlying whorl (instead of the convex surface that the circle would result in).
Figure 3.10: (a) A mathematical Nautilus; (b) cross-section of (a); (c) an optimized (b); (d) a real Ammonite.
Of course, this "theory" in the shell's development can not be proved in the way T. A. Cook, Moseley and others for instance proved the presence a logrithmic spiral in shells. This is due to the fact that we are now moving into domains of evolution which are more complex, in the sense that a lot more factors govern the shape of the aperture, and it is therefore not suitable for a deeper mathematical study.

The model

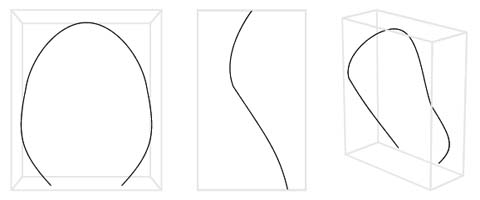
The curve C we have used to generate the surface is shown, from different viewpoints, on figure 3.11.

Figure 3.11: The generating curve of the Nautilus from different viewpoints: front, profile, combined.
The result of coiling the Nautilus' generating curve around the z-axis, with the parameters W = 3, D = 1 and T = 0 is shown on figure 3.12.
Figure 3.12: The Nautilus shell model.

Other kinds of shells, horns

With the above described model, combining Frenet-Serret frames with Raup's Coiling Model and Bézier curves, it is only a matter of will to model any kind of shells. This section is meant as an illustration of this purpose, without going into the details of each specific shell's constructions. We shall only mention that, in some cases, the formula for the seashell has been modified slightly in order to model bumps and ribs, often present on the surfaces. This is actually straightforward. Recall from section 3.1.3 that D is a constant controlling the overall magnification of the C, in particular its dimensions at q = 0. By making it a function of q, we can vary the magnification throughout a revolution, for instance using the bell-shaped function e-pt2. An example of such a shell is the Epitonium scalare, the second figure below.
Astele Armillatum Epitonium Scalare
Ficus Filosa Penion Mandarinus
Thatcheria Mirabilis Nautilus Pompilus
Greater Kudu Wild sheep

Pictures of the models can be found in much greater resolution in the 3D shell and horns gallery.

Discussion

Many attemps to model seashells using a computer have been made, starting from David Raup in 1962. The following models have more or less been based on this one, with some improvements. In particular, Prusinkiewicz et al. [7] added, in 1992, textures to the shell surface, while Cortie [10] made, in 1993, a 16 parameter model which gave more freedom in the orientation of the uvw coordinate system and integrated ribs and bumps explicitely in the formula for the shell. As you may have noticed, these are all very recent works, indicating that modeling of these relatively simple shapes found in nature still reveal great challenge if one wishes to understand them completely.

We shall end this chapter by showing an example of a shell which cannot be modelled using our model or any of the above mentioned. In fact, the lack of self-similarity (due to the sudden change in the apertures shape) makes this, in the essence, impossible.
Figure 3.13: Strombus Listeri.