skelet2.mw
Maple-skelet for Sidefagssuplering
Jens Gravesen
nogle praktiske rutiner:
| > |
a1:=[1,2,3,4,5]; a2:=[5,4,3,2,1]; |
![a1 := [1, 2, 3, 4, 5]](images/skelet2_1.gif)
![a2 := [5, 4, 3, 2, 1]](images/skelet2_2.gif)
Kan "sy" a1 og a2 sammen vha. "seq"-kommandoen:
| > |
[seq( [ a1[i], a2[i] ], i=1..nops(a1))]; |
![[[1, 5], [2, 4], [3, 3], [4, 2], [5, 1]]](images/skelet2_3.gif)
Bernsteinpolynomierne:
| > |
B:=(n,k,t)->binomial(n,k)*(1-t)^(n-k)*t^k; |

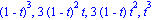
De grundlæggende operatorer:
![R := proc (x) options operator, arrow; x[1 .. -2] end proc](images/skelet2_6.gif)
![L := proc (x) options operator, arrow; x[2 .. -1] end proc](images/skelet2_7.gif)
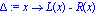
| > |
C:=(x,t)->(1-t)*R(x)+t*L(x); |
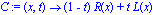
Nogle kontrolpolygoner:
| > |
a:=[[0,0],[1,1],[0,1],[1,0]]; |
![a := [[0, 0], [1, 1], [0, 1], [1, 0]]](images/skelet2_10.gif)
| > |
b:=[[0,0],[0,4],[4,4],[4,0]]; |
![b := [[0, 0], [0, 4], [4, 4], [4, 0]]](images/skelet2_11.gif)
| > |
c:=[[0,0,0],[1,0,0],[1,1,0],[1,1,1],[0,1,1]]; |
![c := [[0, 0, 0], [1, 0, 0], [1, 1, 0], [1, 1, 1], [0, 1, 1]]](images/skelet2_12.gif)
Og de tilsvarende Bezier kurver:
| > |
at:=expand(add(B(3,i,t)*a[i+1],i=0..3)); |
![at := [4*t^3+3*t-6*t^2, -3*t^2+3*t]](images/skelet2_13.gif)
| > |
bt:=expand(add(B(3,i,t)*b[i+1],i=0..3)); |
![bt := [-8*t^3+12*t^2, -12*t^2+12*t]](images/skelet2_14.gif)
| > |
ct:=expand(add(B(4,i,t)*c[i+1],i=0..4)); |
![ct := [4*t^3-2*t^4-6*t^2+4*t, 3*t^4-8*t^3+6*t^2, -3*t^4+4*t^3]](images/skelet2_15.gif)
Differentiationsoperatoren jvf. Sætning 1.9
![[[3, 3], [-3, 0], [3, -3]]](images/skelet2_16.gif)
![[[0, 12], [12, 0], [0, -12]]](images/skelet2_17.gif)
![[[4, 0, 0], [0, 4, 0], [0, 0, 4], [-4, 0, 0]]](images/skelet2_18.gif)
Gradsforøgelse jvf. Sætning 1.12
![[0, 1, 2]](images/skelet2_19.gif)
![[0, 2, 4, 6]](images/skelet2_20.gif)
![[[0, 0], [3/4, 3/4], [1/2, 1], [1/4, 3/4], [1, 0]]](images/skelet2_21.gif)
![[[0, 0], [0, 3], [2, 4], [4, 3], [4, 0]]](images/skelet2_22.gif)
Subdivision:
![[[[0, 0], [1/2, 1/2], [1/2, 3/4], [1/2, 3/4]], [[1/2, 3/4], [1/2, 3/4], [1/2, 1/2], [1, 0]]]](images/skelet2_23.gif)
![[[[0, 0], [0, 2], [1, 3], [2, 3]], [[2, 3], [3, 3], [4, 2], [4, 0]]]](images/skelet2_24.gif)
![[[0, 0], [.5, .5], [.50, .75], [.500, .750], [.50, .75], [.5, .5], [1, 0]]](images/skelet2_25.gif)
![[[0, 0], [0., 1.00], [.2500, 1.7500], [.625000, 2.250000], [1.00000, 2.75000], [1.5000, 3.0000], [2.000, 3.000], [2.5000, 3.0000], [3.00000, 2.75000], [3.375000, 2.250000], [3.7500, 1.7500], [4.00, 1....](images/skelet2_26.gif)
![[[0, 0], [0., 1.00], [.2500, 1.7500], [.625000, 2.250000], [1.00000, 2.75000], [1.5000, 3.0000], [2.000, 3.000], [2.5000, 3.0000], [3.00000, 2.75000], [3.375000, 2.250000], [3.7500, 1.7500], [4.00, 1....](images/skelet2_27.gif)
![[[0, 0], [0., 1.00], [.2500, 1.7500], [.625000, 2.250000], [1.00000, 2.75000], [1.5000, 3.0000], [2.000, 3.000], [2.5000, 3.0000], [3.00000, 2.75000], [3.375000, 2.250000], [3.7500, 1.7500], [4.00, 1....](images/skelet2_28.gif)
| > |
ctr_a:=plots[pointplot](a,connect=true,thickness=2,linestyle=DASH): |
| > |
p1a:=plots[pointplot](subdiv2(a,1),connect=true,thickness=3,color=red): |
| > |
p2a:=plots[pointplot](subdiv2(a,2),connect=true,thickness=3,color=green): |
| > |
p3a:=plots[pointplot](subdiv2(a,3),connect=true,thickness=3,color=blue): |
| > |
plots[display]([ctr_a,p1a,p2a,p3a],scaling=constrained); |
![[Plot]](images/skelet2_29.gif)
| > |
atp:=plot([op(at),t=0..1],color=magenta): |
| > |
plots[display]([ctr_a,p3a,atp],scaling=constrained); |
![[Plot]](images/skelet2_30.gif)
| > |
ctr_b:=plots[pointplot](b,connect=true,thickness=2,linestyle=DASH): |
| > |
p1b:=plots[pointplot](subdiv2(b,1),connect=true,thickness=3,color=red): |
| > |
p2b:=plots[pointplot](subdiv2(b,2),connect=true,thickness=3,color=green): |
| > |
p3b:=plots[pointplot](subdiv2(b,3),connect=true,thickness=3,color=blue): |
| > |
plots[display]([ctr_b,p1b,p2b,p3b],scaling=constrained); |
![[Plot]](images/skelet2_31.gif)
| > |
btp:=plot([op(bt),t=0..1],color=magenta): |
| > |
plots[display]([ctr_b,p3b,btp],scaling=constrained); |
![[Plot]](images/skelet2_32.gif)
![b2 := [[0, 0], [0, 3], [2, 4], [4, 3], [4, 0]]](images/skelet2_33.gif)
| > |
p3b2:=plots[pointplot](subdiv2(b2,3),connect=true,thickness=3,color=magenta): |
| > |
plots[display]([p3b,p3b2],scaling=constrained); |
![[Plot]](images/skelet2_34.gif)
| > |
ctr_c:=plots[pointplot3d](c,connect=true,thickness=2,linestyle=DASH,color=black): |
| > |
p1c:=plots[pointplot3d](subdiv2(c,1),connect=true,thickness=3,color=red): |
| > |
p2c:=plots[pointplot3d](subdiv2(c,2),connect=true,thickness=3,color=green): |
| > |
p3c:=plots[pointplot3d](subdiv2(c,3),connect=true,thickness=3,color=blue): |
| > |
plots[display]([ctr_c,p1c,p2c,p3c],scaling=constrained,axes=boxed); |
![[Plot]](images/skelet2_35.gif)
| > |
ctp:=plots[spacecurve]([op(ct),t=0..1],color=magenta): |
| > |
plots[display]([ctr_c,p3c,ctp],scaling=constrained,axes=boxed); |
![[Plot]](images/skelet2_36.gif)
Nogle hjælpefunktioner:
skalar-produktet:
| > |
return add(x[k]*y[k], k=1..nops(x)); |
![dot := proc (x, y) local k; return add(x[k]*y[k], k = (1 .. nops(x))) end proc](images/skelet2_37.gif)
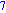
længde af en vektor:
| > |
vectorlength:=x->sqrt(dot(x,x)); |
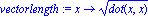

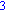
længde af vektorer i en liste kan fås ved brug af "map" kommandoen:
| > |
map(vectorlength, [ [1,1], [3,4], [1,2] ]); |
![[2^(1/2), 5, 5^(1/2)]](images/skelet2_42.gif)
kryds-produktet:
| > |
cross := (x,y)-> convert(linalg[crossprod](x,y), list); |
, list) end proc](images/skelet2_43.gif)
| > |
cross([1,0,0],[0,1,0]); |
![[0, 0, 1]](images/skelet2_44.gif)
Funktion til udregning af polygon længde:
| > |
s:=map(vectorlength, s); |
| > |
return [0,seq(add(s[l], l=1..k), k=1..nops(s))]; |
![[0, 2^(1/2), 1+2^(1/2), 1+2*2^(1/2)]](images/skelet2_45.gif)
![[0, 4, 8, 12]](images/skelet2_46.gif)
Funktion til udregning af buelængde af Bezier kurve
subdivider m gange og brug polylength
| > |
BezierArcLength:=proc(x,m) |
Funktion til udregning af krumning jvf. Sætning 2.14
| > |
curvature:=proc(r1,r2) # r1 er 1. afledede og r2 er 2. afledede |
| > |
curvature([1,0],[1,1]); |
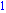
| > |
curvature([2,0],[4,4]); |
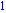
| > |
curvature([2,2,0],[1,1,1]); |

Funktion til udregning af krumning langs Bezier kurve
differentier, gradsforøg, subdiv og brug "curvature"
| > |
BezierCurvature:=proc(x,m) |
| > |
BezierArcLength(a,0),BezierCurvature(a,0);
BezierArcLength(a,1),BezierCurvature(a,1); |
![[0, 2^(1/2), 1+2^(1/2), 1+2*2^(1/2)], [1/6*2^(1/2), 5/2*2^(1/2), 5/2*2^(1/2), 1/6*2^(1/2)]](images/skelet2_50.gif)
![[0, .7071067812, .9571067812, .9571067812, .9571067812, 1.207106781, 1.914213562], [1/6*2^(1/2), .8944271910, 4.000000000, Float(undefined), 4.000000000, .8944271910, 1/6*2^(1/2)]](images/skelet2_51.gif)
![[0, .7071067812, .9571067812, .9571067812, .9571067812, 1.207106781, 1.914213562], [1/6*2^(1/2), .8944271910, 4.000000000, Float(undefined), 4.000000000, .8944271910, 1/6*2^(1/2)]](images/skelet2_52.gif)
Funktion til fremstilling af krumningsplot
| > |
BezierCurvaturePlot:=proc(x,m,farve) |
| > |
s:=BezierArcLength(x,m); |
| > |
k:=BezierCurvature(x,m); |
| > |
sk:=[seq([s[i],k[i]], i=1..nops(s))]; |
| > |
plots[pointplot](sk,connect=true,thickness=3,color=farve): |
| > |
kb0:=BezierCurvaturePlot(b,0,red): |
| > |
kb1:=BezierCurvaturePlot(b,1,green): |
| > |
kb3:=BezierCurvaturePlot(b,3,blue): |
| > |
kb5:=BezierCurvaturePlot(b,5,magenta): |
| > |
plots[display]([kb0,kb1,kb3,kb5]); |
![[Plot]](images/skelet2_53.gif)
![dbt := [-24*t^2+24*t, -24*t+12]](images/skelet2_54.gif)
![d2bt := [-48*t+24, -24]](images/skelet2_55.gif)
| > |
dsdt:=sqrt(dbt[1]^2+dbt[2]^2); |
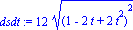
| > |
s:=subs(u=t,int(dsdt,t=0..u)); |
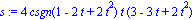
| > |
kappa:=simplify((dbt[1]*d2bt[2]-dbt[2]*d2bt[1])/dsdt^3); |
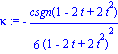
| > |
kbt:=plot([s,-kappa,t=0..1],color=black): |
| > |
plots[display]([kbt,kb5]); |
![[Plot]](images/skelet2_59.gif)
| > |
ka0:=BezierCurvaturePlot(a,0,red): |
| > |
ka1:=BezierCurvaturePlot(a,1,green): |
| > |
ka3:=BezierCurvaturePlot(a,3,blue): |
| > |
ka5:=BezierCurvaturePlot(a,5,magenta): |
krumningen er uendelig for t=1/2 så for at se noget begrænser vi y-aksen til 100.
| > |
plots[display]([ka0,ka1,ka3,ka5],view=0..10); |
![[Plot]](images/skelet2_60.gif)
En Maple plotte fejl?
![[Plot]](images/skelet2_61.gif)
| > |
kc0:=BezierCurvaturePlot(c,0,red): |
| > |
kc1:=BezierCurvaturePlot(c,1,green): |
| > |
kc3:=BezierCurvaturePlot(c,3,blue): |
| > |
kc5:=BezierCurvaturePlot(c,5,magenta): |
| > |
plots[display]([kc0,kc1,kc3,kc5]); |
![[Plot]](images/skelet2_62.gif)
Funktion til udregning af torsion jvf. Sætning 2.28
| > |
torsion:=proc(r1,r2,r3) # r1, r2, r3 er de 3 første afledede |
| > |
torsion([1,0,0],[0,1,0],[0,0,1]); |
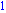
| > |
torsion([1,1,0],[0,2,0],[1,0,3]); |

Funktion til udregning af torsion langs Bezier kurve
differentier, gradsforøg, subdiv og brug "torsion"
| > |
BezierTorsion:=proc(x,m) |
Funktion til fremstilling af torsionsplot
| > |
BezierTorsionPlot:=proc(x,m,farve) |
| > |
s:=BezierArcLength(x,m); |
| > |
st:=[seq([s[i],t[i]], i=1..nops(s))]; |
| > |
plots[pointplot](st,connect=true,thickness=3,color=farve): |
| > |
t0:=BezierTorsionPlot(c,0,red): |
| > |
t1:=BezierTorsionPlot(c,1,green): |
| > |
t3:=BezierTorsionPlot(c,3,blue): |
| > |
t5:=BezierTorsionPlot(c,5,magenta): |
| > |
plots[display]([t0,t1,t3,t5]); |
![[Plot]](images/skelet2_65.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[[[0, 0], [1/2, 1/2], [1/2, 3/4], [1/2, 3/4]], [[1/2, 3/4], [1/2, 3/4], [1/2, 1/2], [1, 0]]]](images/skelet2_23.gif)
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/skelet2_29.gif)
![[Plot]](images/skelet2_30.gif)
![[Plot]](images/skelet2_31.gif)
![[Plot]](images/skelet2_32.gif)
![]()
![[Plot]](images/skelet2_34.gif)
![[Plot]](images/skelet2_35.gif)
![[Plot]](images/skelet2_36.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/skelet2_53.gif)
![]()
![]()
![]()
![]()
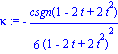
![[Plot]](images/skelet2_59.gif)
![[Plot]](images/skelet2_60.gif)
![[Plot]](images/skelet2_61.gif)
![[Plot]](images/skelet2_62.gif)
![]()
![]()
![[Plot]](images/skelet2_65.gif)