MATHEMATICS OF A NAUTILUS SHELL

A logarithmic spiral (Figure 1) can be characterized as a plane curve where the tangent vector at each point P of the curve makes a constant angle u with the direction from a fixed point O (the spiral point) to the curve point (click for animation). For that reason logarithmic spirals often appear in growth phenomena in nature, where the growth is combined with a turning through a fixed angle, as in the spiral curves in a sunflower. The seeds in a sunflower follows a growth form that biologists call phyllotaxis: new seeds grow forward at points further and further away from the center while at the same time the points turn a fixed angle.

A similar growth phenomenon lies behind the occurrence of a logarithmic spiral in connection with the Nautilus shell, where exponential growth is combined with a fixed turning. The construction of the Nautilus shell will be explained below.

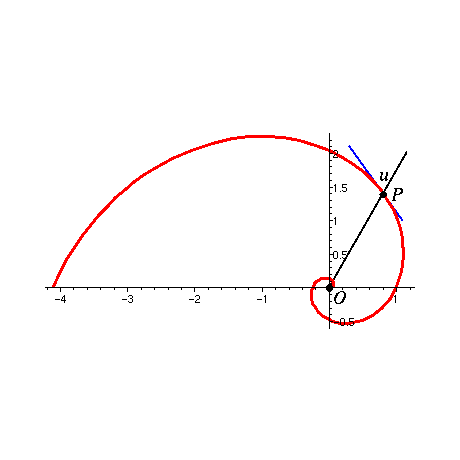
Figure 1

At each point P of a plane curve, in particular of a logarithmic spiral, there is a well defined circle that among all circles is the best possible approximation to the curve: the so-called circle of curvature, with center C in the center of curvature, and the radius of curvature as radius. The construction is depicted in Figure 2.

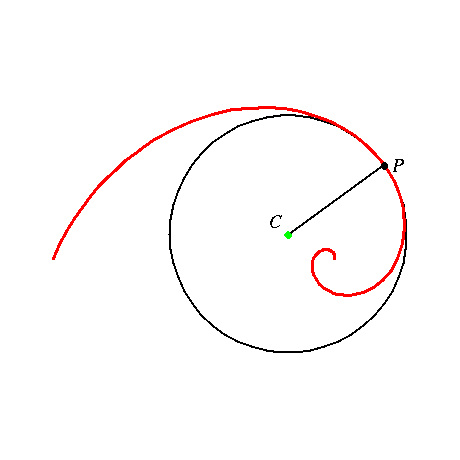
Figure 2

The centers of curvature make a curve, which is called the evolute of the curve; the green curve in Figure 3. For the logarithmic spiral, the evolute is again a logarithmic spiral. It can be constructed by rotating the logarithmic spiral through a right angle and multiplying by cotangent of u.

Symmetrical to the evolute with respect to the logaritmic spiral, there is another logaritmic spiral, which we call the exterior evolute. The exterior evolute is depicted in Figure 3 together with a number of ribbons connecting corresponding points on the evolute and the exterior evolute.

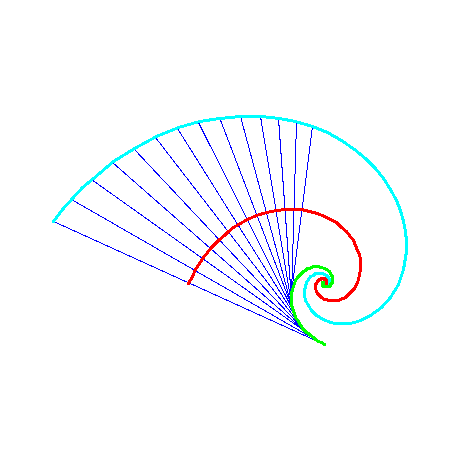
Figure 3

For exactly one angle u, approximately 69.5 degrees, the evolute and the exterior evolute of the logarithmic spiral fit each others; cf. Figure 4. In the following we use this unique angle in the logarithmic spiral.

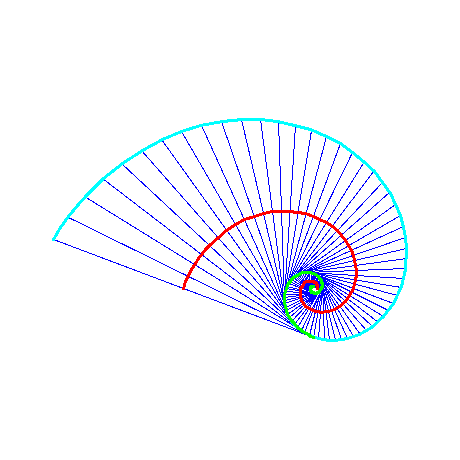
Figure 4

If the circles of curvature of the logarithmic spiral are placed so that they are centered on the curve and are othogonal both to the curve and to the plane of the curve (click for animation), then a Nautilus shell appears. Shown in Figure 5 (click for animation) in tranparent form, and in Figure 6 (click for animation) in complete form.

Figure 5

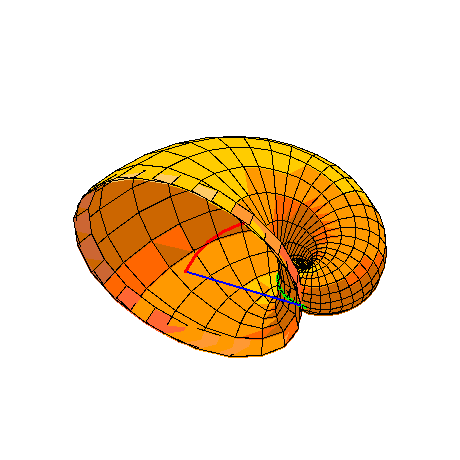
Figure 6

The angle 69.5 degrees is very close to half the golden angle (approximately 137.5 degrees), which arises by dividing the circumference of a circle in the golden ratio. For the logarithmic spiral behind the Nautilus shell it is therefore approximately true that the line through the spiral point and the curve point divides the circle of curvature in the golden ratio; cf. Figure 7 (click for animation). It should also be remarked that the slightly smaller angle u given by half the golden angle will leave a gap between the evolute and the exterior evolute. Such a gap will allow for thickness of the Nautilus shell and thereby supports the conjecture that the golden ratio is connected with this growth phenomenon in nature.

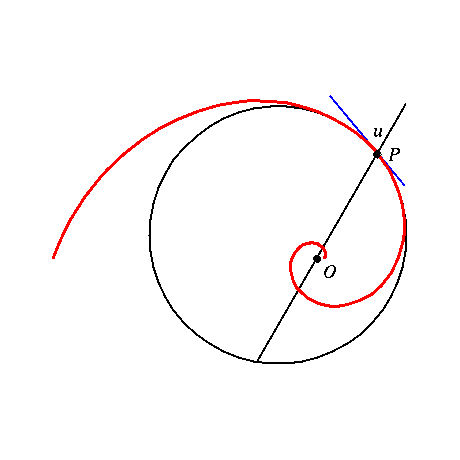
Figure 7

The bottom half and the top half of the Nautilus shell is shown in respectively Figure 8 and Figure 9.

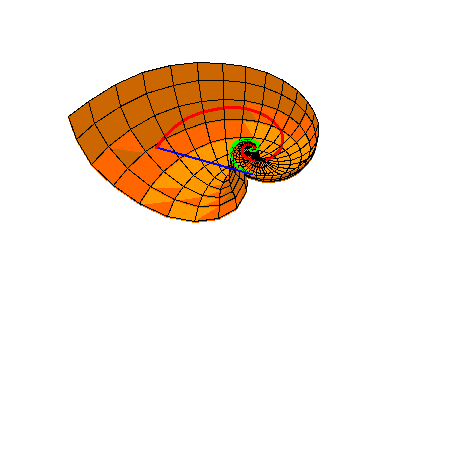
Figure 8

Figure 9