 |
 |
|
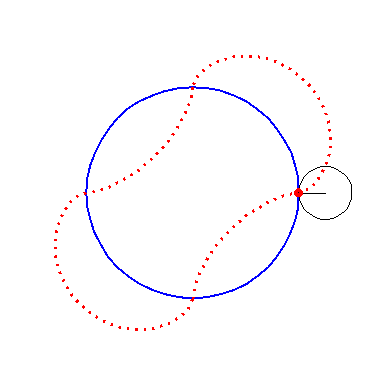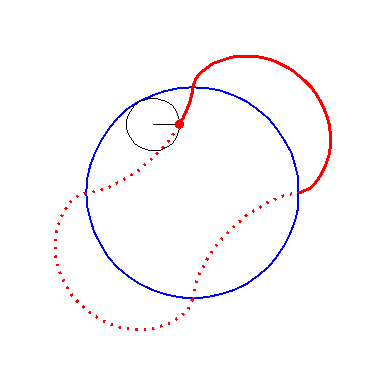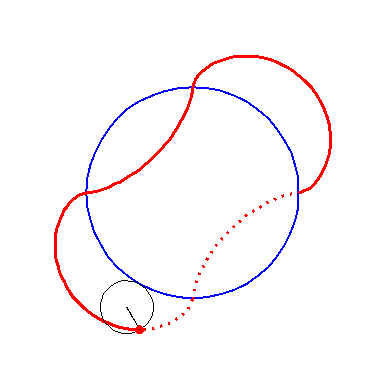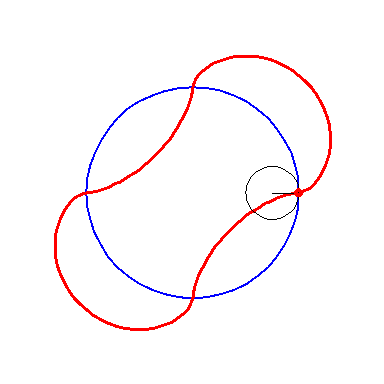
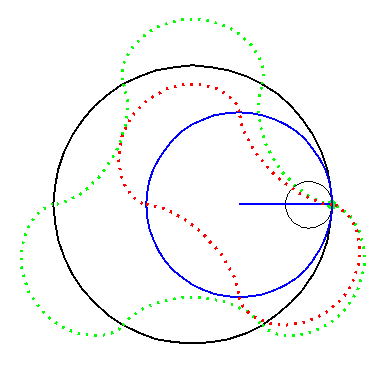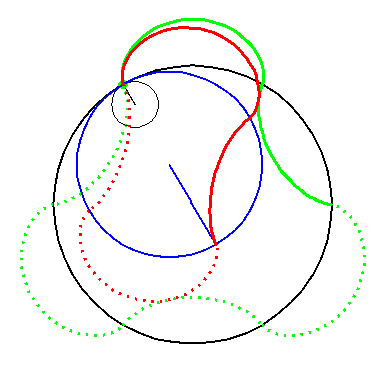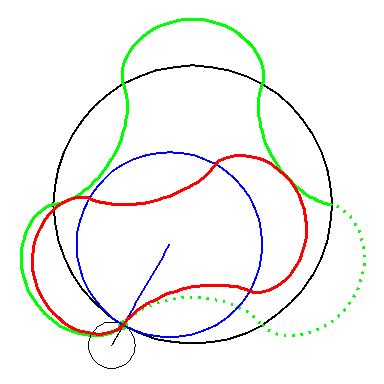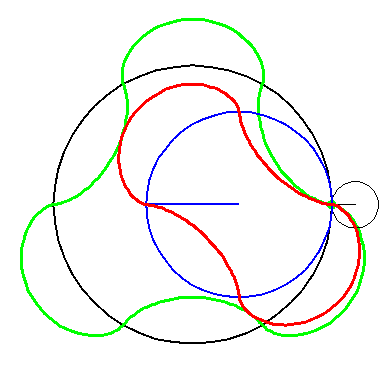
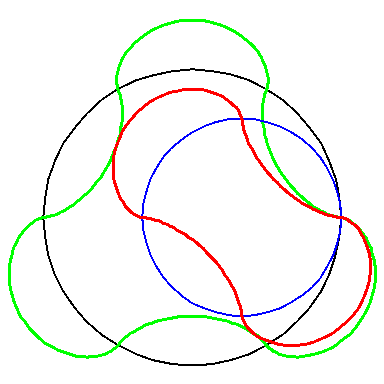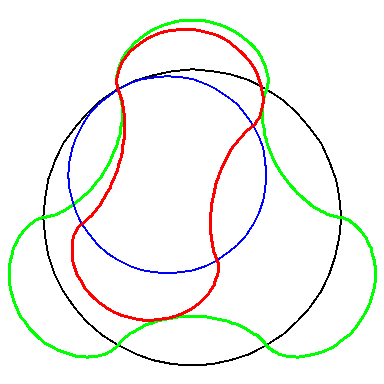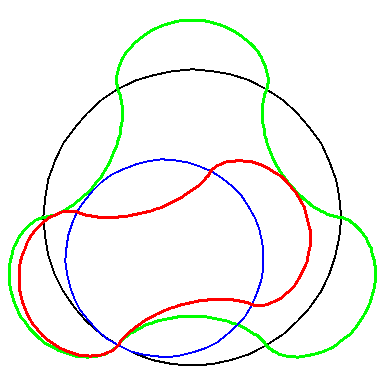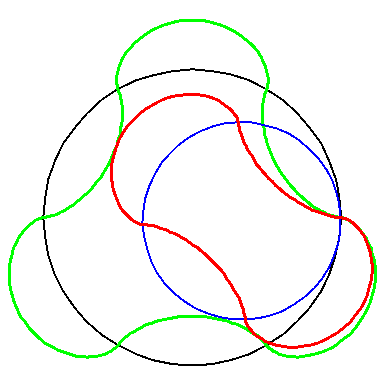
When the black circle with radius 1 rolls on the outside of the blue
circle with radius 4 the fixed red point on the small circle traces
out an arc of the epi-cycloid E4 and when it rolls
on the inside the blue circle it traces out an arc of the hypo-cycloid
H4. The four arcs form the curve
A2.
|
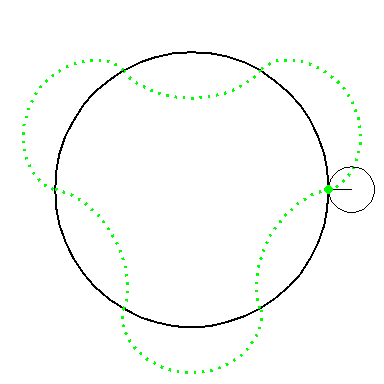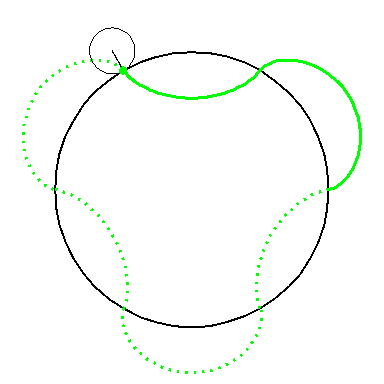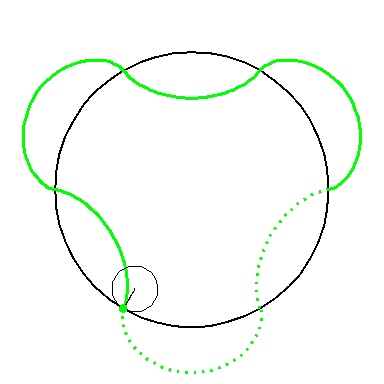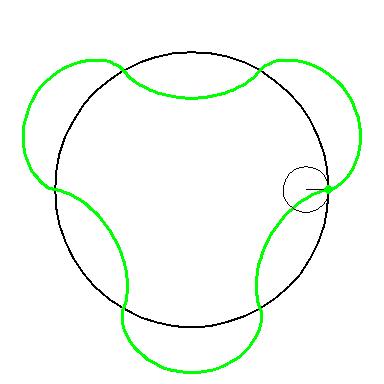
When the circle with radius 1 rolls on the outside of the circle with
radius 6 the fixed green point on the small circle traces out arcs of
the epi-cycloid E6 and when it rolls on the inside
it traces out arcs of hypo-cycloid H6. The six arcs
form the curve A3.
|
 |
 |
|
When the blue circle with radius 4 rolls inside the black circle with
radius 6 the moving red curve A2 is enveloped by
the green curve A3.
|
|
 |
 |
 |
 |
|
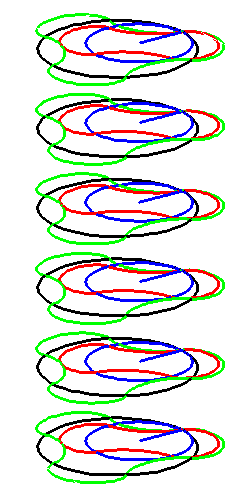
The construction above is lifted to horizontal
planes z = constant.
|
The blue circle is rolled a distance proportional to the height
z. Observe that the blue circles no longer are above each other.
|
By rotating the picture in each horizontal plane the blue circles can
be positioned over each other such as to form a blue cylinder inside a
black cylinder.
|
The motion generated by letting the blue cylinder roll inside the
black cylinder is in each horzontal plane the same as before.
|
|
 |
 |
 |
 |
|
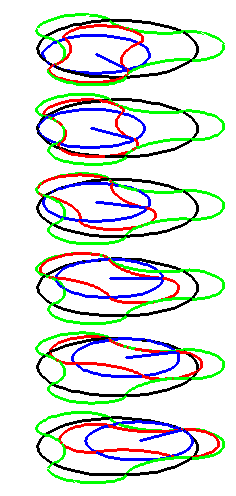
A series of pump chambers are formed and they move upwards as rigid
bodies under the motion generated by the letting the blue cylinder
roll inside the black cylinder.
|























