Furthermore, the endpoints of H2 traces out H3.
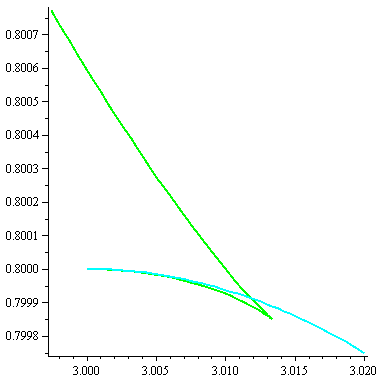
If we zoom in on the area in the circle, where the semicircle meet the offset of the hypo-cycloid, then we clearly see the cusp. Notice the different scaling on the axis.
 |
 |
 |
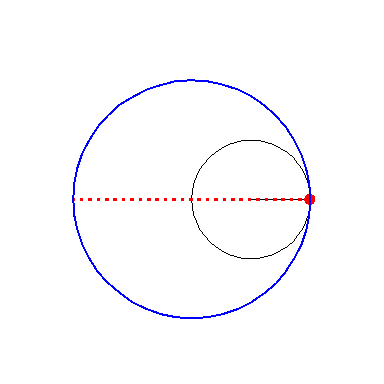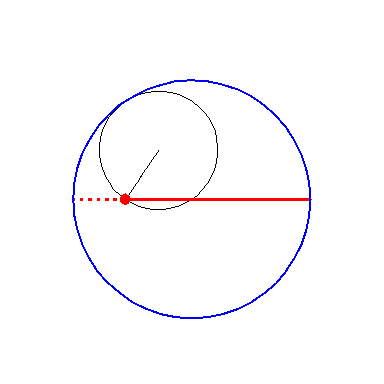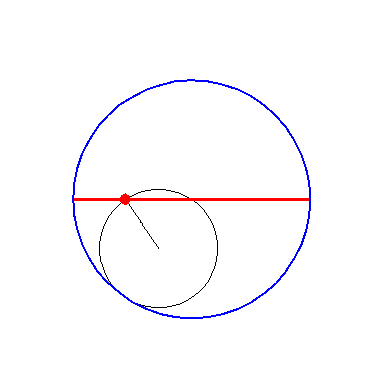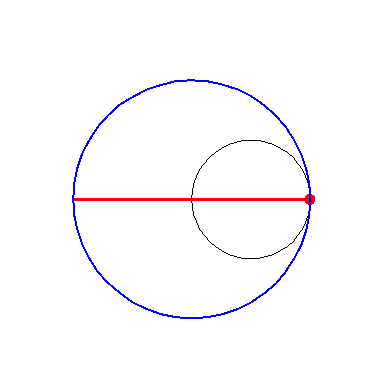
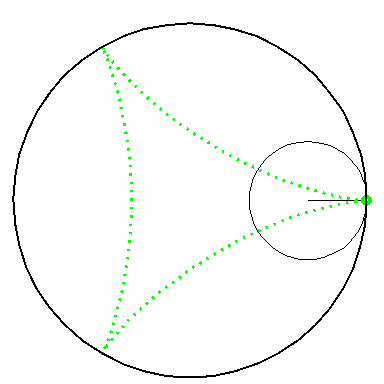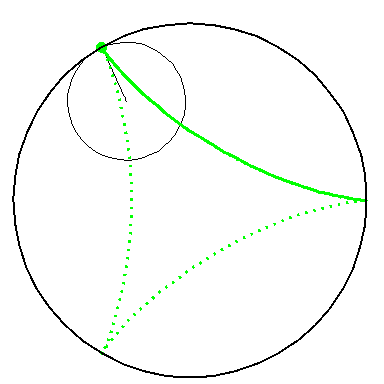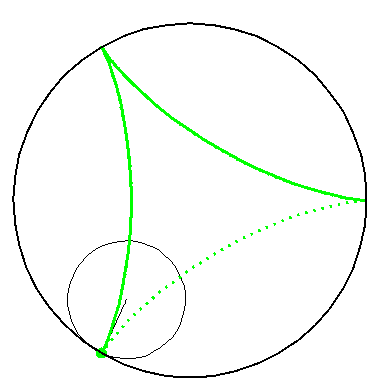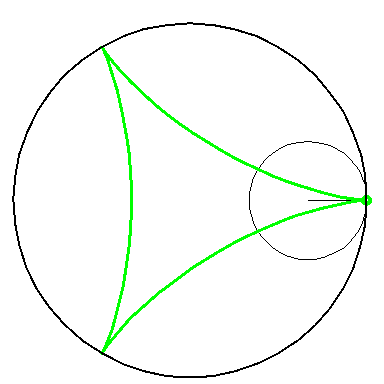
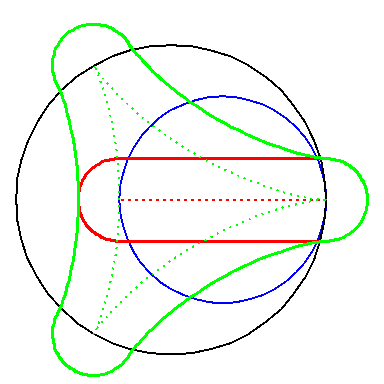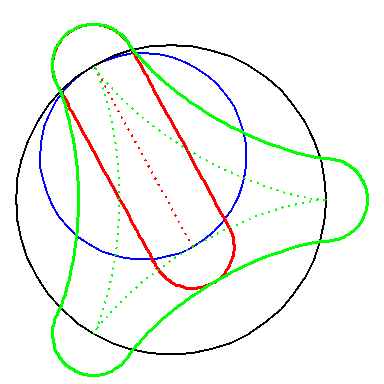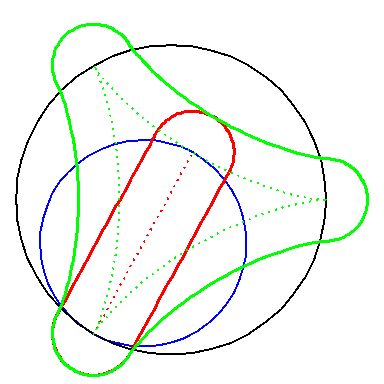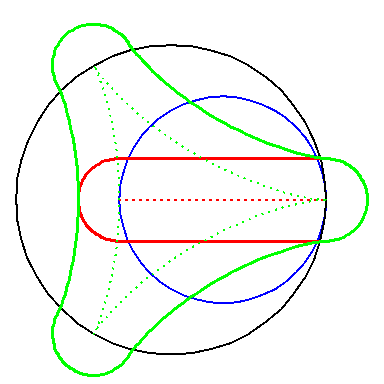
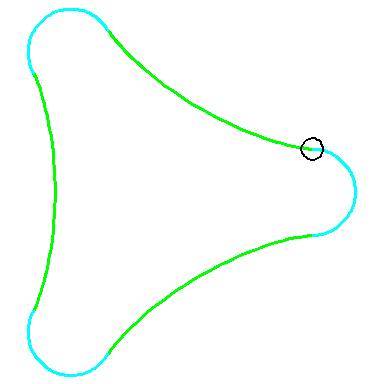
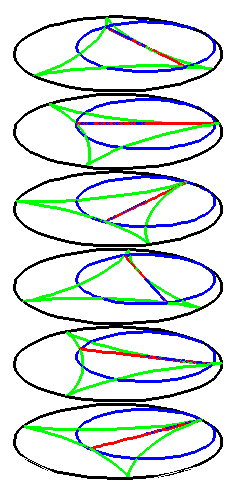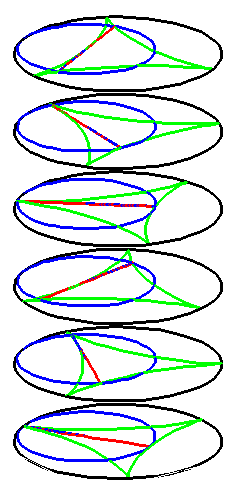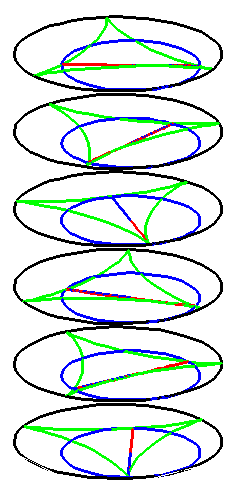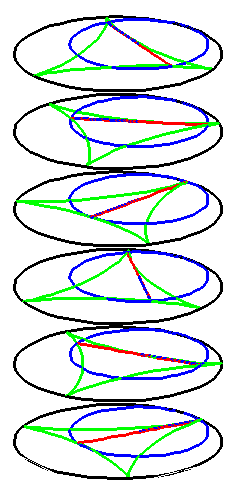
| By rolling the black circle with radius 1 inside the blue circle with radius 2 the fixed red point on the small circle traces out the red diameter H2 in the blue circle. | By rolling the circle with radius 1 inside the circle with radius 3 the fixed green point on the small circle traces out the green hypo-cycloid H3 in the big circle. |
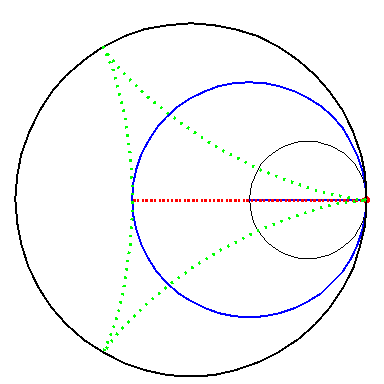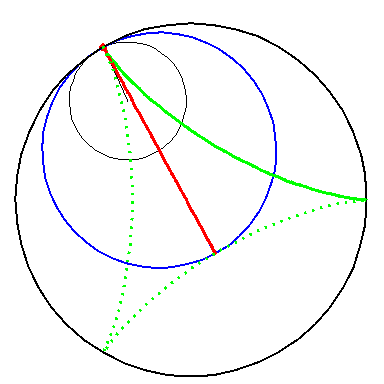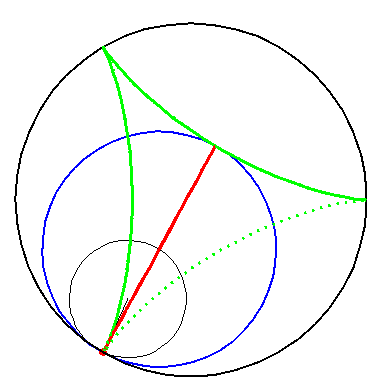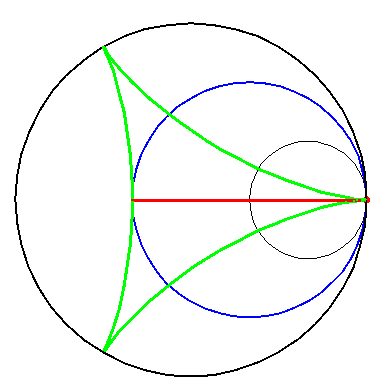
When the blue circle with radius 2 rolls inside the black circle with
radius 3 the moving red diameter H2 is enveloped by
the green hypo-cycloid H3.
Furthermore, the endpoints of H2 traces out H3. |
 |
 |
 |
| In an attempt to avoid the cusps we can offset the construction. We take offsets of the hypo-cycloids and attach semicircles. |
But the hypo-cycloid H3 has infinite curvature at
the cusps, so an offset has cusps too.
If we zoom in on the area in the circle, where the semicircle meet the offset of the hypo-cycloid, then we clearly see the cusp. Notice the different scaling on the axis. |
|
 |
 |
 |
 |
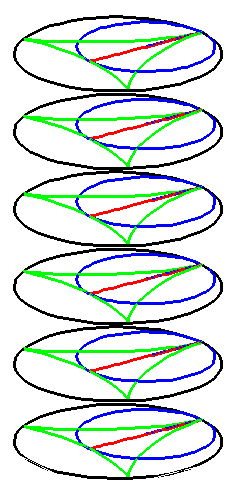
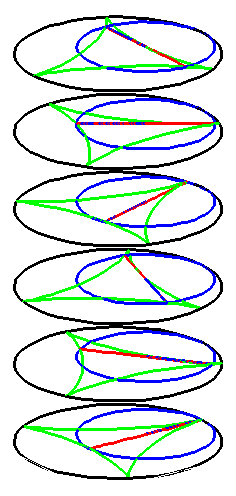
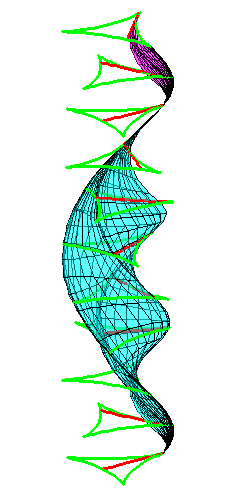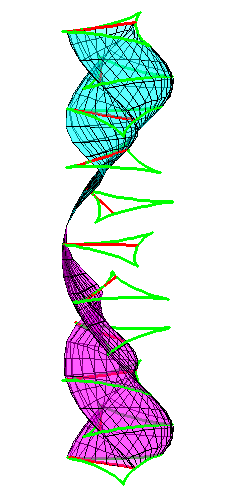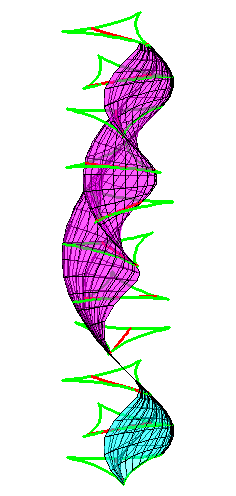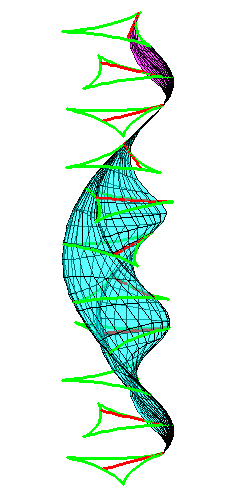
| The construction above is lifted to horizontal planes z = constant. | The blue circle is rolled a distance proportional to the height z. Observe that the blue circles no longer are above each other. | By rotating the picture in each horizontal plane the blue circles can be positioned over each other such as to form a blue cylinder inside a black cylinder. | The motion generated by letting the blue cylinder roll inside the black cylinder is in each horzontal plane the same as before. |
 |
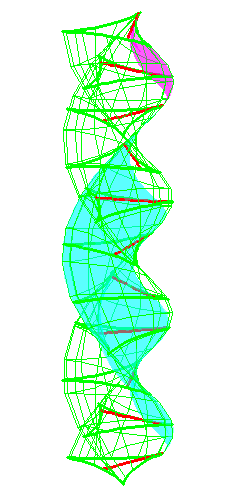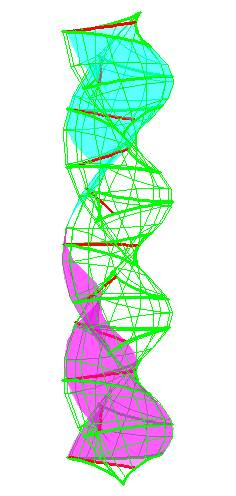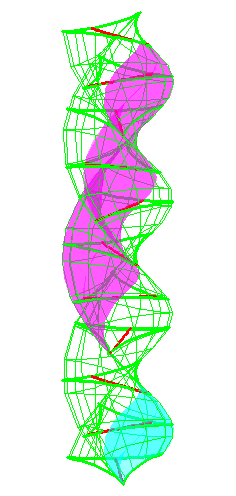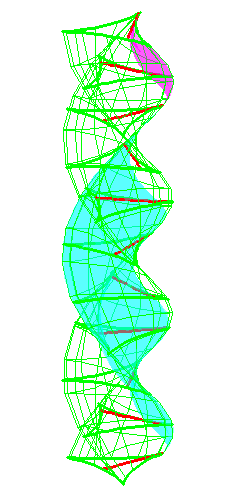 |
 |
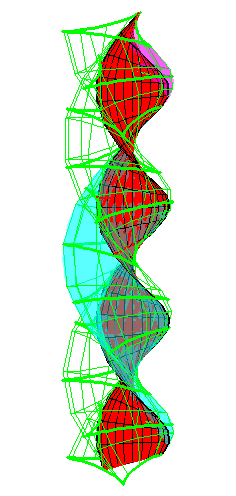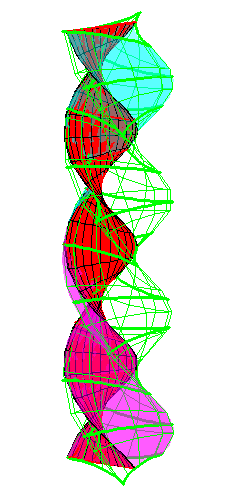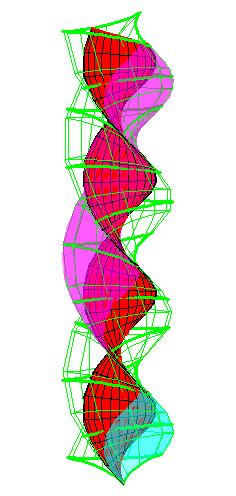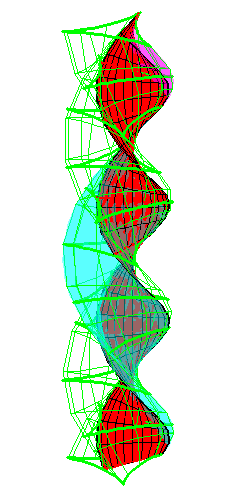 |
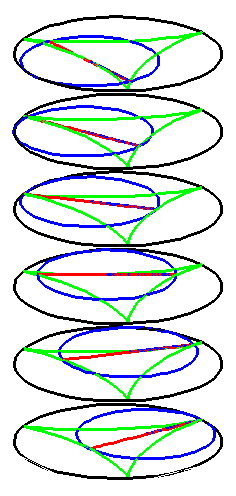
| A series of pump chambers are formed and they move upwards as rigid bodies under the motion generated by the letting the blue cylinder roll inside the black cylinder. | |||