
Furthermore, the cusps of E3 traces out E2.

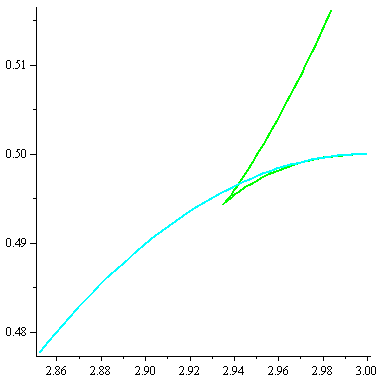
If we zoom in on the area in the circle, where the semicircle meet the offset of the epi-cycloid, then we clearly see the cusp. Notice the different scaling on the axis.
 |
 |
 |
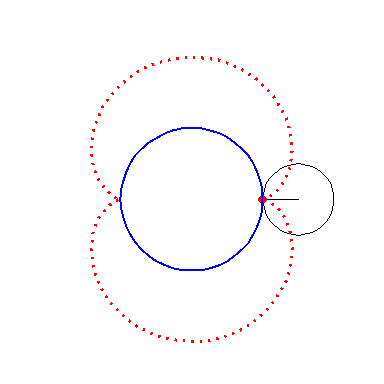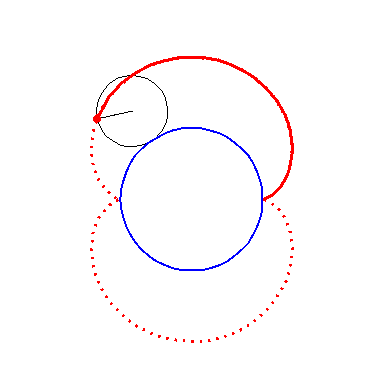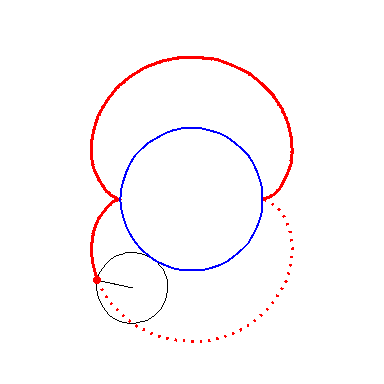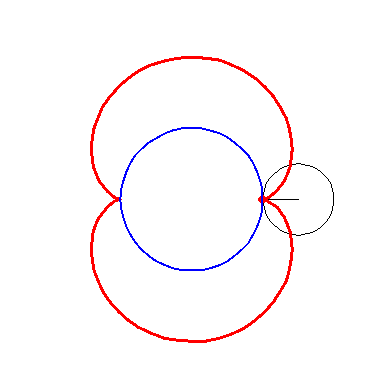
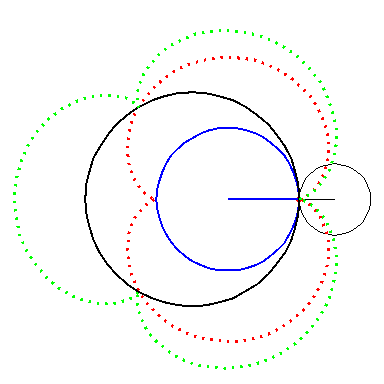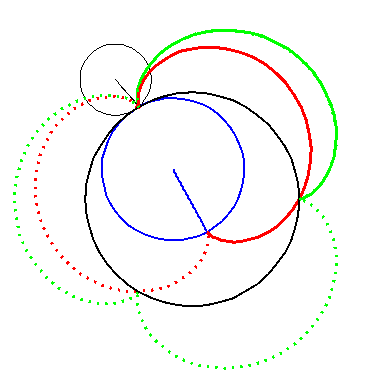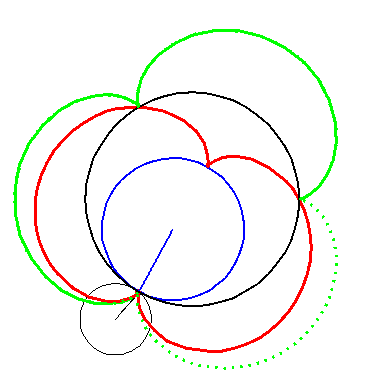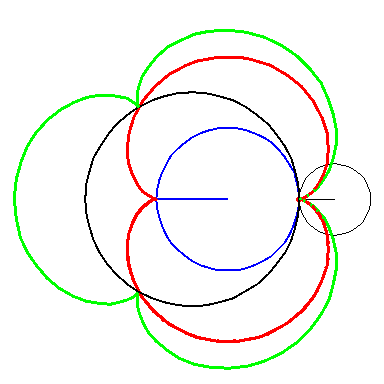
| By rolling the black circle with radius 1 on the outside of the blue circle with radius 2 the fixed red point on the small circle traces out the red epi-cycloid E2. | By rolling the circle with radius 1 on the outside of the circle with radius 3 the fixed green point on the small circle traces out the green epi-cycloid E3. |
When the blue circle with radius 2 rolls inside the black circle with
radius 3 the moving red epicycloid E2 is enveloped by
the green epi-cycloid E3.
Furthermore, the cusps of E3 traces out E2. |
 |
 |
 |
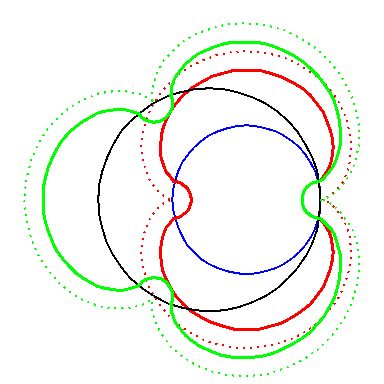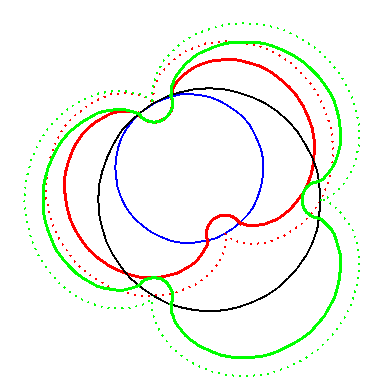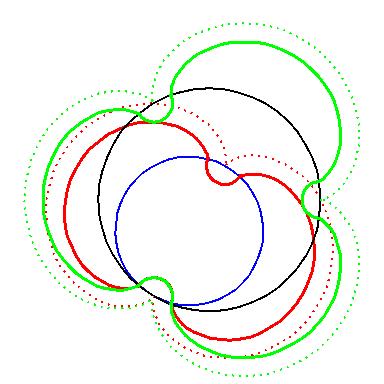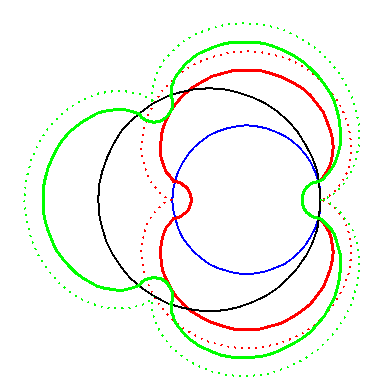
| In an attempt to avoid the cusps we can offset the construction. We take offsets of the epi-cycloids and attach semicircles. |
But the epi-cycloid E3 has infinite curvature at
the cusps, so an offset has cusps too.
If we zoom in on the area in the circle, where the semicircle meet the offset of the epi-cycloid, then we clearly see the cusp. Notice the different scaling on the axis. |
|
 |
 |
 |
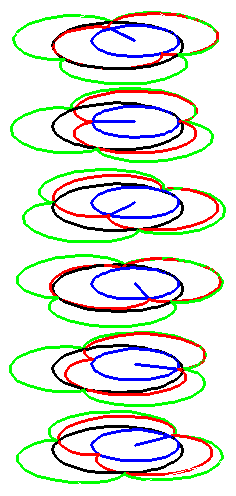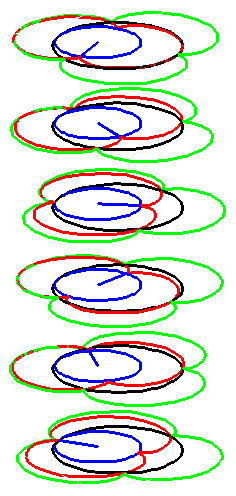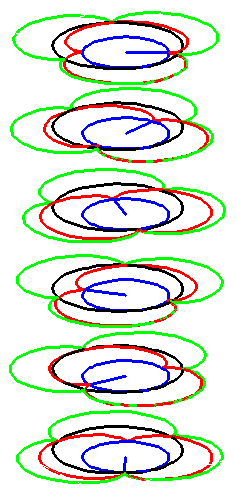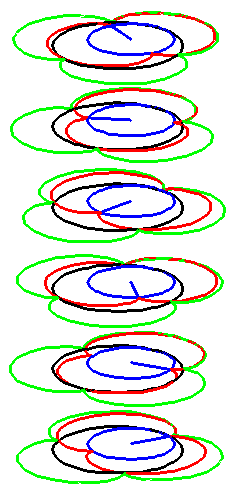 |
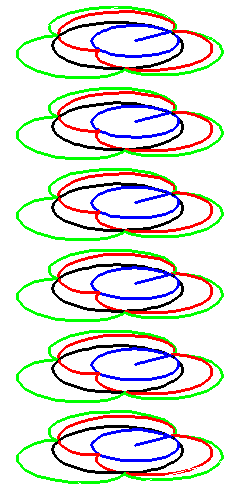
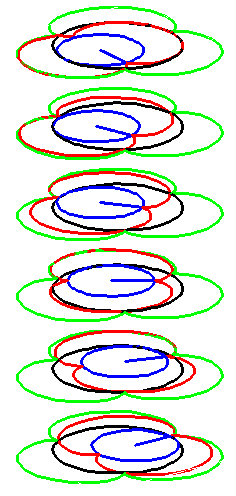
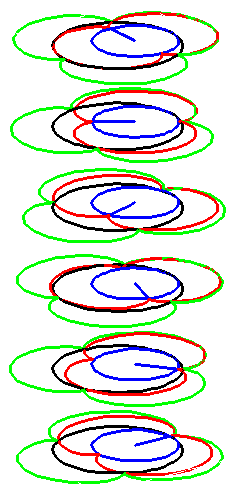
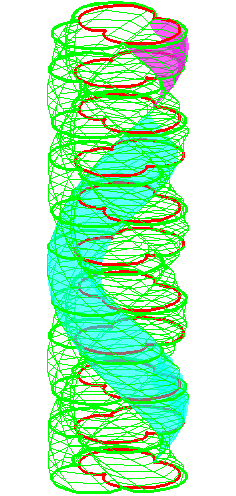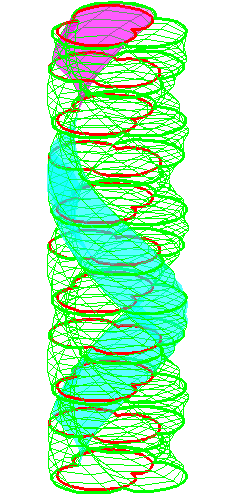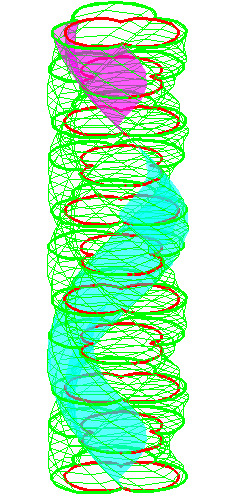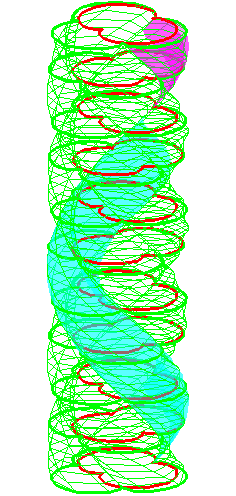
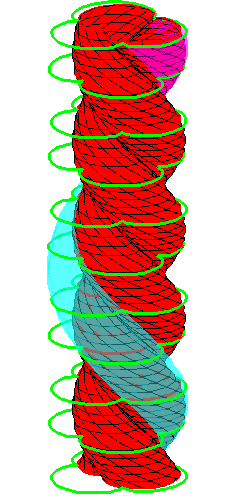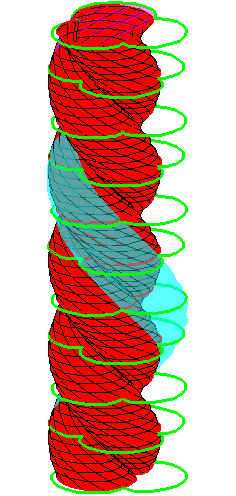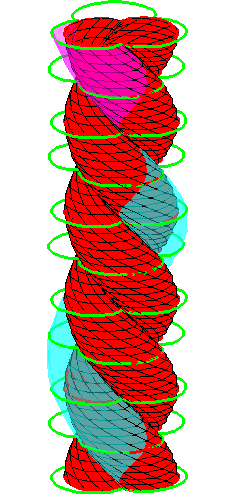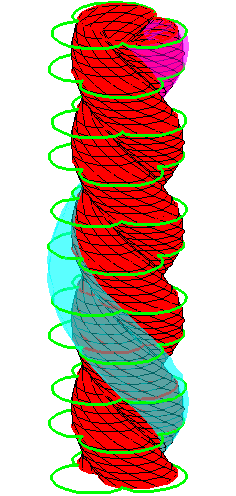
| The construction above is lifted to horizontal planes z = constant. | The blue circle is rolled a distance proportional to the height z. Observe that the blue circles no longer are above each other. | By rotating the picture in each horizontal plane the blue circles can be positioned over each other such as to form a blue cylinder inside a black cylinder. | The motion generated by letting the blue cylinder roll inside the black cylinder is in each horzontal plane the same as before. |
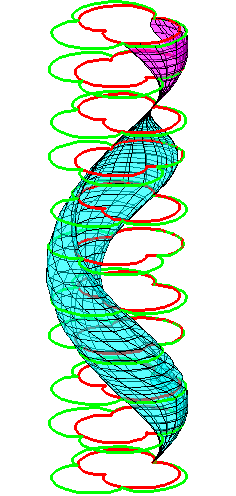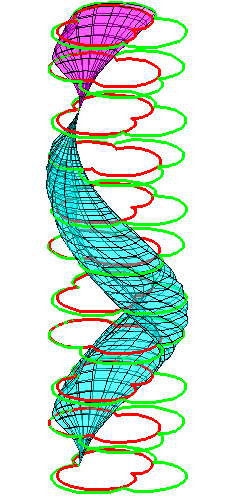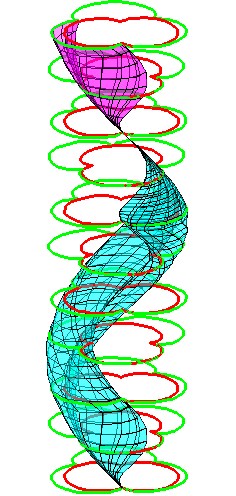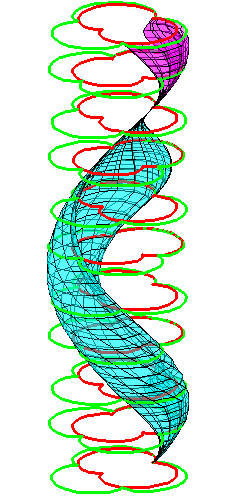 |
 |
 |
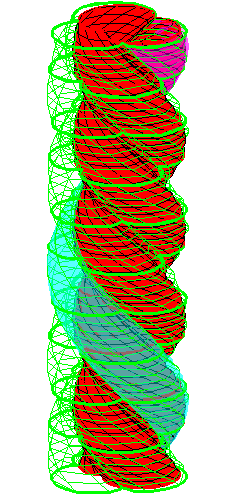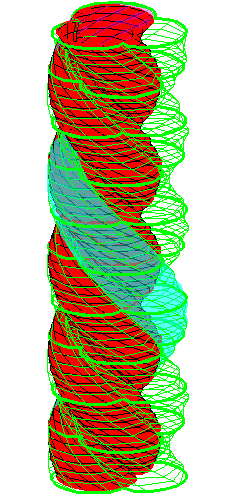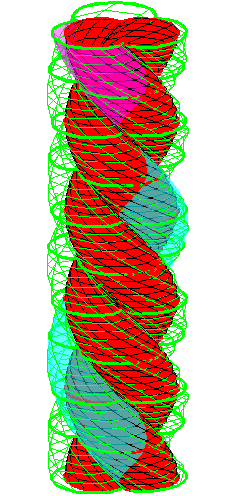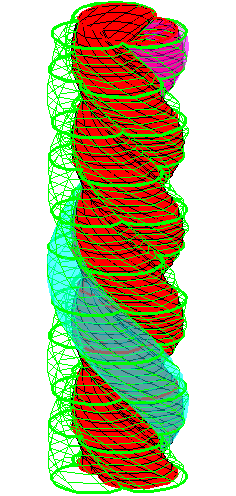 |
| A series of pump chambers are formed and they move upwards as rigid bodies under the motion generated by the letting the blue cylinder roll inside the black cylinder. | |||