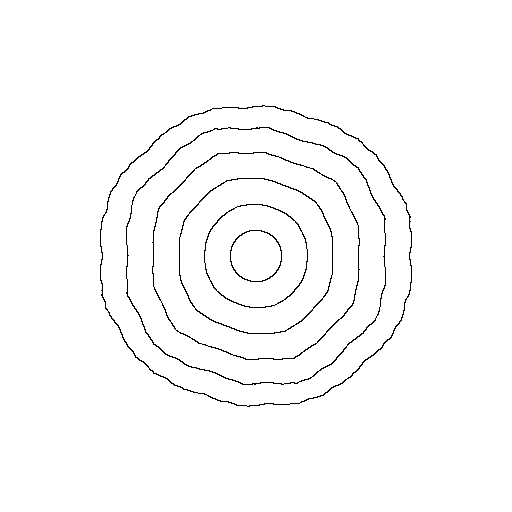
Consider the family of rational maps \[ f_{\lambda,a}(z) = z^2 \frac{az + 1}{a + z} \] where \(\lambda\) is a complex number different from zero and \(a\) is complex. Fix a giving (Brjuno) rotation number. The parameters where the corresponding rational map possesses a Herman ring with the given rotation number forms a disk. The subset of parameters where we fix the modulus forms a real-analytic curve. Approximations the projection to the \(a\)-coordinate of such curves for the rotation number equal to the golden mean is shown in the figure below:

To draw curves of constant modulus we approximate the modulus by \[ \frac{1}{n} \sum_{j=0}^{n-1} \log \left(\frac{f^j(\omega_2)} {f^j(\omega_1)} \right) . \] where \(\omega_1\) is the inner critical point, and \(\omega_2\) is the outer.
In the following animation we show the dynamical plane as we follow the outer curve around in parameter space. The black circle is the unit circle. The moving black points are the first \(10^5\) iterates of the two critical points.

Now set the rotation number to be [30, 1, 1, ...] = 1/(30+γ), where γ is the golden mean. Even if more difficult this time around, we still approximate curves in the Arnold disk:
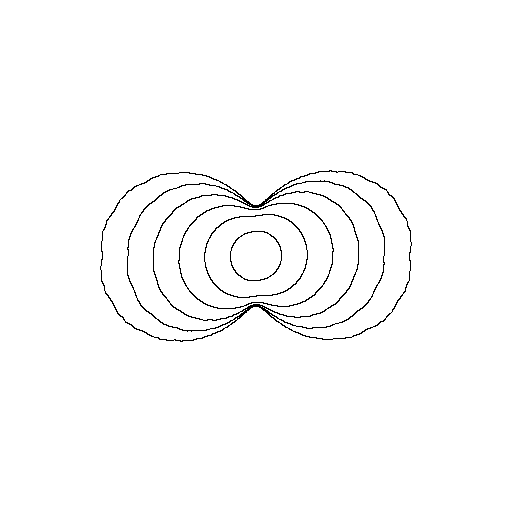
It seems that the disk is somehow pinched. Again we make an animation following the outer curve around:

We draw the same types of pictures, but this time in logarithmic coordinates. With a somwhat bigger modulus than the previous picture, we get the following animiation:

Following a curve closer to the boundary of the Arnold Disks, with get Herman rings with smaller moduli.
