Gymnasieopgave: Varmeledning
| > | restart;interface(warnlevel=0):with(plots): |
1. Differentialligningen
| > | lign:=C*diff(T(t),t)=P-U*A*(T(t)-T0); |
![]()
Ligningen er en 1. ordens lineær differentialligning. Vi bruger MAPLE
| > | los:=dsolve({lign,T(0)=T0},T(t)); |
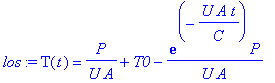
Heraf ses at for
![]() gælder
gælder
| > | Tu:=P/U/A+T0; |
![]()
Måles Tu - T0 = P/UA kan U bestemmes.
Talværdier:
| > | V:=0.5^3; |
| > | A:=6*0.5^2; |
| > | lambda:=4.1*10^(-2); |
| > | L:=2.0*10^(-2); |
| > | U:=lambda/L; |
| > | rho:=1.20; |
| > | cp:=1.01*10^3; |
| > | m:=rho*V; |
| > | C:=cp*m; |
| > | T0:=20.0; |
| > | P:=60.0; |
| > | tau:=C/U/A; |
| > | cp := 1010.00; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | los:=dsolve({lign,T(0)=T0},T(t)); |

| > | los1:=subs(t=t*60,rhs(los));evalf(los1); |
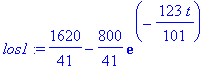
![]()
| > | s0:=textplot([[0.75,41.5,"t"],[2.9,24," t = 0.82"]],font=[SYMBOL]): |
| > | s:=textplot([[1.5,32,"Temperaturkurve for flamingokasse"],[1.5,24,"Tidskonstant"],[3.4,3,"[min] , tid "],[0.1,45.0,"[C] , temperatur"],[3.4,24,"min"]],align={RIGHT}): |
| > | p2:=plot(20.0+19.512*60*t/tau,t=0..0.85,0..45,linestyle=2): |
| > | p0:=plot(40.0,t=0..4,0..40,linestyle=4): |
| > | p1:=plot(los1,t=0..4.5,0..40): |
| > | display(s0,s,p1,p2,p0); |
![[Maple Plot]](images/varmeledning21.gif)
| > |