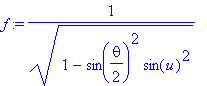
Gymnasieopgave: Pendulet

>    restart;with(plots): 

Warning, the name changecoords has been redefined

******************************************************************************

Formlen for svingningstiden er

>    f:=1/sqrt(1-sin(theta/2)^2*sin(u)^2);

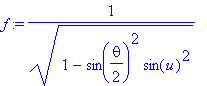
f := 1/((1-sin(1/2*theta)^2*sin(u)^2)^(1/2))

>    T:=4*sqrt(g/l)*Int(f,u=0..Pi/2);

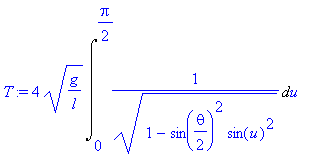
T := 4*(g/l)^(1/2)*Int(1/((1-sin(1/2*theta)^2*sin(u)^2)^(1/2)),u = 0 .. 1/2*Pi)

Opgave 1

 For theta = 0 finder vi f = 1 altså bliver intgralet = 2 pi  

>    limit(T,theta=0);

2*(g/l)^(1/2)*Pi

Opgave 2

Vi laver en Taylorudvikling af integranden og sætter

>    t:=sin(theta/2)^2*sin(u)^2;

>    h:=(1-x)^(-1/2);

>    p:=taylor(h,x=0,2);

>    p:=convert(p,polynom);

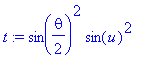
t := sin(1/2*theta)^2*sin(u)^2

h := 1/((1-x)^(1/2))

p := series(1+1/2*x+O(x^2),x,2)

p := 1+1/2*x

Vi indsætter det tilnærmede udtryk i T og integrerer

>    p:=subs(x=t,p);

>    T_ny:=4*sqrt(g/l)*int(p,u=0..Pi/2);

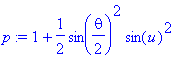
p := 1+1/2*sin(1/2*theta)^2*sin(u)^2

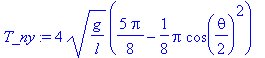
T_ny := 4*(g/l)^(1/2)*(5/8*Pi-1/8*Pi*cos(1/2*theta)^2)

Vi indsætter l = 1.00 meter  og g = 9,81 meter i T og plotter udtrykket

>    T_ny:=evalf(subs(g=9.81,l=1.0,T_ny));

>    T:=subs(g=9.81,l=1.0,T);

T_ny := 24.59939267-4.919878534*cos(.5000000000*theta)^2

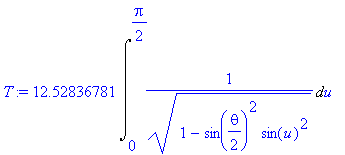
T := 12.52836781*Int(1/((1-sin(1/2*theta)^2*sin(u)^2)^(1/2)),u = 0 .. 1/2*Pi)

Et plot for theta  = 0.. pi  viser hvor god tilnærmelsen er

>    plot([T_ny,T],theta=0..Pi/2,0..25,numpoints=100);

[Maple Plot]

>   

>