Gymnasieopgave: Kastet.

>	restart;interface(warnlevel=0):with(plots):with(plottools):with(linalg):

Spørgsmål 1.

Vi har givet

>	v0:=14.0;alpha:=evalf(60.0*Pi/180.0);g:=9.81;

Tiden t1 hvor strålen rammer facaden x1= 9 meter borte:

>

x1:=9.0;

>	t1:=x1/(v0*cos(alpha));

y1 koordianten er:

>

y0:=1.5;

>	y1:=y0+v0*sin(alpha)*t1-1/2*g*t1^2;

>	y:=x->1.5+tan(alpha)*x-9.81/2.0/v0^2/cos(alpha)^2*x^2;

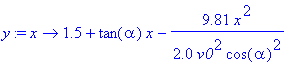
>	hus:=polygon([[9.0,0.0], [15.0,0.0], [15.0,9.0],[9.0,9.0],[9.0,0.0]], color=grey, linestyle=1, thickness=2):

>	p:=plot(y(x),x=0..9,color=blue,thickness=3):

>	display(p,hus,scaling=constrained,view=[-0.2..16.50,0.0..11.0]);

Spørgsmål 2.

Hastigheden af vandet er nu

>

v0:=18.0;

>	eval(y(x));

Strålen bliver nu

>	p:=plot(y(x),x=0..30,color=blue,thickness=3):

>	display(p,hus,scaling=constrained,view=[-0.2..30.0,0.0..15.0]);

AK, vi skyder over huset! Hvad gør vi ???

Ballistiske kurver

>	restart:interface(warnlevel=0):with(plots):with(linalg):

Newtons 2. lov opstilles i projektion på x- og y-retningen:

>	lign:={diff(x(t),t$2)=-c/m*diff(x(t),t)*sqrt(diff(x(t),t)^2+diff(y(t),t)^2),diff(y(t),t$2)=-g-c/m*diff(y(t),t)*sqrt(diff(x(t),t)^2+diff(y(t),t)^2)};

Begyndelsesbetingelserne

>	begynd:={x(0)=0.0,D(x)(0)=v0*cos(theta),y(0)=0.0,D(y)(0)=v0*sin(theta)};

Talværdier:

>	m:=0.180;g:=9.81;c:=evalf(0.5/8*1.2*Pi*0.008^2);v0:=828.0;dt:=0.001;alpha:=0.125;theta:=Pi/180.0*alpha;

Numerisk løsning af differentialligningssystmet med en 4. ordens Runge-Kutta metode:

>	f:=dsolve(lign union begynd,{x(t),y(t)},numeric);

Er tiden t = 1.0 bliver løsningen:

>

f(1.0);

Vi har altså brug for det 2. og den 4. element i løsningen:

>	f(1)[2];f(1)[4];

For at plotte løsningen gemmes koordinaterne i en vektor med 1000 pladser

>	xy:=vector(1000);

>	for i from 1 to 1000 do xy[i]:=[rhs(f(i*dt)[2]),rhs(f(i*dt)[4])] end do:

vi ser kun på tisdintervallet 100 dt  = 400* 0,001 sekund = 0,4 sek.

>	s:=[xy[u]$u=1..400]:

>	p1:=plot([s,[v0*cos(theta)*t,-1/2*g*t^2+v0*sin(theta)*t,t=0..400*dt]]):

>	ss:=textplot([[250,0.02,"x i meter"],[10,0.16,"y i meter"]],align={ABOVE,RIGHT}):

>	display(p1,ss);

Hastigheden i afstanden 300 meter findes for t = 0,36675

>	f(0.36675);

>

>