Gymnasieopgave: Jordskælvssvingninger

>    restart;

>    with(plots): 

Warning, the name changecoords has been redefined

Beton:

>    rho:=2400.0;

>    E:=2.40*10^10;

>    Bt:=30.0*10^6;

>    Bb:=5.0*10^6;

rho := 2400.0

E := .2400000000e11

Bt := 30000000.0

Bb := 5000000.0

Stål:

>    #rho:=7800.0;

>    #E:=20.0*10^10;

>    #Bt:=250.0*10^6;

Højhus:

>    h:=50.0;

>    a:=25.0;

>    t:=0.3;

>    A:=a^2-(a-3*t)^2;

>    V:=A*h;

h := 50.0

a := 25.0

t := .3

A := 44.19

V := 2209.500

Ser vi bort fra de indvendige vægge, får vi

>    It:=1/12*(a^4-(a-2*t)^4);

It := 3014.28920

En mere nøjagtig beregning giver

>    It:=1/12*(a^4-(a-2*t)^4)+1/12*0.3*(a-2*t)^3+1/12*(a-3*t)*0.3^3;

>    ymax:=a/2;

>    Wt:=It/ymax;

>    m:=V*rho;

It := 3377.513025

ymax := 12.50000000

Wt := 270.2010420

m := 5302800.000

Frekvens:

>    me:=0.25*m;

>    k:=3*E*It/h^3;

>    omega0:=sqrt(k/me);

>    f0:=omega0/(2.0*evalf(Pi));

>    T0:=1/f0;

>    tau:=0.25;

>    f:=1/tau;

>    gain:=x->1/abs(1-(x/f0)^2);

>    gain(f);

me := 1325700.000

k := 1945447502.

omega0 := 38.30779281

f0 := 6.096874585

T0 := .1640184632

tau := .25

f := 4.000000000

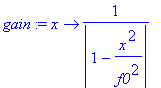
gain := x -> 1/abs(1-x^2/(f0^2))

1.755719389

Udbøjning:

>    delta0:=0.08;

>    udsving:=delta0*gain(f);

>    delta:=udsving-delta0;

>    P:=delta*k;

>    M:=h*P;

>    sigma_max:=M/Wt;

>    sigma_brud:=0.75*Bt;

delta0 := .8

udsving := 1.404575511

delta := .604575511

P := 1176169918.

M := .5880849590e11

sigma_max := 217647184.0

sigma_brud := 22500000.00

>    plot([gain(x),[[0.0,gain(f)],[f,gain(f)]],[[f,0.0],[f,gain(f)]]],x=0.0..2*f0,0.0..5.0,title="absolut udsving af top af højhus",color=black);

[Maple Plot]

>    plot([(x/f0)^2*gain(x),[[0.0,(f/f0)^2*gain(f)],[f,(f/f0)^2*gain(f)]],[[f,0.0],[f,(f/f0)^2*gain(f)]]],x=0.0..2*f0,0.0..5.0,title="relativ udsving af top af højhus",color=black);

[Maple Plot]