Gymnasieopgave : Søforurening 

> restart;with(plots):
 

Warning, the name changecoords has been redefined
 

***************************************************************************** 

1. Den lineære differentialligningen er , se H&OL side 120. 

> lign:=diff(c(t),t)+a(t)*c(t)/V=m(t)/V;
 

lign := (diff(c(t), t))+a(t)*c(t)/V = m(t)/V 

Og den generelle løsning er: 

> dsolve(lign,c(t));
 

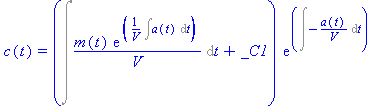
c(t) = (Int(m(t)*exp(1/V*Int(a(t), t))/V, t)+_C1)*exp(Int(-a(t)/V, t)) 

Grænseværdien c_0 er  i  ton/km^3  og V i km^3 . 

 

> c_0=0.1*10^(-9)/(10^(-3))*(10^9/10^3);
 

> V:=2;
 

c_0 = .1000000000 

V := 2 

2. Find c(t) , når a(t) = a_0 , m(t) = m_0 , V = 2  

> lign1:=subs(a(t)=1,m(t)=m_0,lign);
 

lign1 := (diff(c(t), t))+1/2*c(t) = m_0/2 

Løsningen er 

> s1:=dsolve({lign1,c(0)=0},c(t));
 

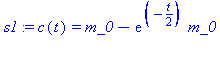
s1 := c(t) = m_0-exp(-t/2)*m_0 

> plot(rhs(s1/m_0),t=0..20);
 

Plot 

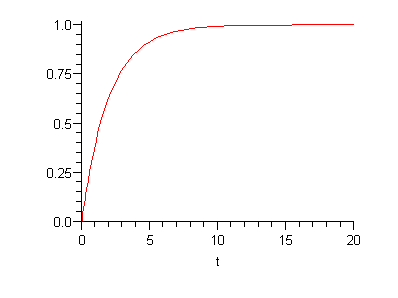
Af løsningen ses, at m_0 < c_0 a_0 =  0.10 ton/år . 

3. Vi opgiver nu m(t) og a(t) 

> m:=t->1/(1+t)^2;
 

m := proc (t) options operator, arrow; 1/((1+t)^2) end proc 

> a:=t->1/(1+t);eval(lign);
 

a := proc (t) options operator, arrow; 1/(1+t) end proc 

(diff(c(t), t))+1/2*c(t)/(1+t) = 1/(2*(1+t)^2) 

2. Den partikulære løsning h(0) = h0 . 

> s2:=dsolve({lign,c(0)=0},c(t));
 

s2 := c(t) = -1/(1+t)+1/((1+t)^(1/2)) 

> plot(rhs(s2),t=0..20);
 

Plot 

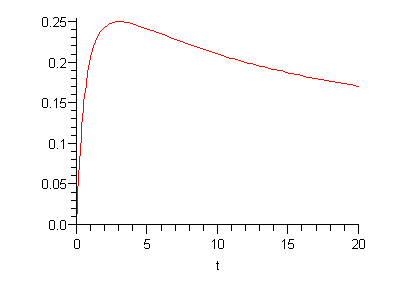
Størsteværdien bliver 

> cmax:=evalf(maximize(rhs(1.0*s2),t=0..4));
 

cmax := .2500000000 

>
 

>