Gymnasieopgave : Faldskærmsudspring 

>	restart;with(plots):with(DEtools):

 

>	assume(a,positive);assume(g,positive);assume(m,positive);

 

>	assume(t,real);assume(v(t),real);

 

Warning, the name changecoords has been redefined
 

***************************************************************************** 

1. Den ulineære differentialligning for faldskærmen er 

>	lign:=diff(v(t),t)=g-a/m*v(t)^2;

 

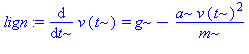
Og den generelle løsning er: 

>	dsolve(lign,v(t));

 

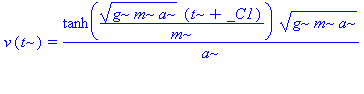
Den partikulære løsning for v(0) = 0 er 

>	l0:=dsolve({lign,v(0)=0},v(t));

 

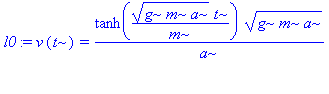
Grænseværdien for t -> 0 

>	lg:=limit(rhs(l0),t=infinity);

 

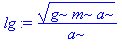
2. Find v(t) , når m = 90 , g = 9,81 og a = 18,7 

>	lign1:=subs(a=18.7,m=90.0,g=9.81,lign);

 

Løsningen er 

>	s1:=evalf(dsolve({lign1,v(0.0)=0.0},v(t)));

 

Grænseværdien er 

>	lg:=evalf(subs(a=18.7,m=90.0,g=9.81,lg));

 

>

%*3.6;

 

d.v.s. ca 25 km/h. 

Plot af løsningen 

>	plot(rhs(s1),t=0..3);

 

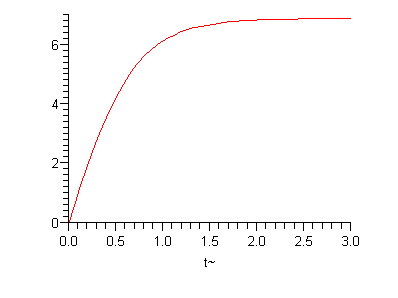
3. Hvis v(0)=20 m/s 

>	Digits:=20;

 

>	s2:=dsolve({lign1,v(0)=20},v(t));

 

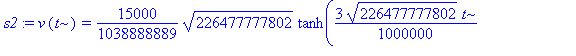
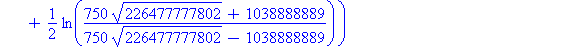
MAPLES løsningen indeholder et imaginært tal og kan ikke plottes umiddelbart, derfor lidt krumspring: 

>	s2:=expand(rhs(s2)):

 

>	s2:=evalf(simplify(s2));

 

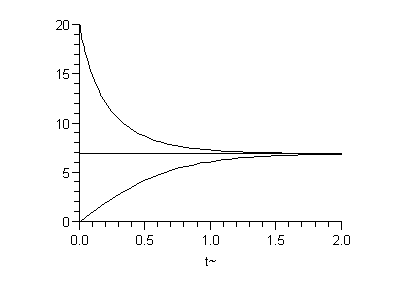
Her plottes de 2 begyndelsesbetingelser v(0) = 0 og v(0) = 20 . 

>	plot({rhs(s1),lg,s2},t=0..2,0..20,color=black);

 

>

 

>