![[Maple Plot]](images/bjaelkeboejning1.gif)
Gymnasieopgave : Mini-projekt i bjælkebøjning.
| > | restart;with(plots):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
Vi har givet en bjælke med længden L , der er belastet med en kraft F på midten. Vi benytter her kommandoen arrow
| > | s:=textplot([[8,5,"F"],[8,-2.2,"L"],[-1,0,"A"],[17,0,"B"]]): |
| > | l0:=arrow([0,-3],vector([16,0]), .05, .5, 0.05, color=black): |
| > | l00:=arrow([1,-3],vector([-1,0]), .05, .5, 0.8, color=black): |
| > | l1 := arrow([0,0],[16,0], .3, .0, .0, color=green): |
| > | l2 := arrow([8,4],vector([0,-3.8]), .3, .8, .2, color=red): |
| > | l3:=plot([[-1,-1.86],[1,-1.86],[0,-0.15],[-1,-1.86]],-1..17): |
| > | l4:=plot([[15,-1.86],[17,-1.86],[16,-0.15],[15,-1.86]]): |
| > | p1:=plot((4*(x/16)^3-3*(x/16)),x=0..8,linestyle=3,numpoints=3): |
| > | p2:=plot((4*((16-x)/16)^3-3*((16-x)/16)),x=8..16,linestyle=3,numpoints=3): |
| > | display(s,p1,p2,l0,l00,l1,l2,l3,l4,axes=none,scaling=constrained); |
![[Maple Plot]](images/bjaelkeboejning1.gif)
For at lave et plot af y'''(x) , må y'''(x) være ikke være givet ved symboler
| > | s:=textplot([[2,9,"y'''(x)"],[-1,1,"A"],[17,1,"B"],[-1,10,"y"],[19,1,"x"],[4,5,"F/(2EIt)"],[12,-5,"- F/(2EIt)"]]): |
| > | lv:=arrow([0,0],vector([20,0]), .05, .5, 0.05, color=black): |
| > | ll:=arrow([0,0],vector([0,10]), .05, .5, 0.1, color=black): |
| > | V:=piecewise(0<x and x<8,4,8<x and x<16,-4,0); |
| > | pp:=plot(V,x=0..20,color=black): |
| > | display(s,pp,lv,ll,l1,l3,l4,axes=none,scaling=constrained); |
![V := PIECEWISE([4, 0 < x and x < 8],[-4, 8 < x and x < 16],[0, otherwise])](images/bjaelkeboejning2.gif)
![[Maple Plot]](images/bjaelkeboejning3.gif)
1. Nedbøjningskurven for 0 < x < L/2 .
I appendiks nederst i dette MAPLE WORK SHEET kan du se, hvorledes opgaven kan løses ved brug af kommandoen piecewise til at definere en stykvis kontinuert funktion .
Her regner vi kun på en bjælke i intervallet 0 < x < L/2 .
Kraften kaldes F . Inertimomnetet af bjælkens tværsnit kaldes It . Elasticitetetsmodulen for træ kaldes E .
Den 3. afledede af nedbøjningen y3(x) = F/(2*E*It) eller
| > | y3:=x->F/(2*E*It); |
![]()
Den 2. afledede af nedbøjningen er y2(x) er krumningen, og der gælder, at y2(0) = 0 . Vi finder y2(x) ved bestemt integration
| > | y2:=x->int(y3(t),t=0..x);eval(y2(x)); |
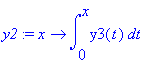
![]()
Den 1. afledede af nedbøjningen er y1(x) er hældninge, og der gælder, at y1(L/2) = 0 . Vi finder y1(x) ved bestemt integration
| > | y1:=x->int(y2(t),t=L/2..x);eval(y1(x)); |
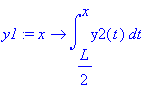
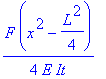
Nedbøjningen er y(x) , og der gælder, at y(0) = 0 . Vi finder y(x) ved bestemt integration
| > | y:=x->int(y1(t),t=0..x);eval(y(x)); |
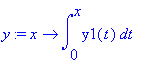
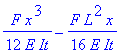
Nedbøjningen på midten for x = L/2 bliver
| > | y(L/2); |
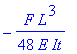
2. Tværsnittets inertimoment eller arealmomnet af 2. orden It.
Vi regner med at tværsnittet har højden h ig bredden b.
| > | s:=textplot([[1.2,1.0,"z"],[2.8,-0.4,"y"],[-0.4,4.6,"z"],[2.4,2.2,"dz"],[0.6,4.4,"h/2"],[0.6,-4.4,"-h/2"],[2.5,0.4,"b/2"],[-2.5,0.4,"-b/2"]]): |
| > | lv:=arrow([-5,0],vector([8,0]), .05, .3, 0.05, color=black): |
| > | ll:=arrow([0,-5],vector([0,10]), .05, .3, 0.05, color=black): |
| > | lz:=arrow([1,0],vector([0,2]), .02, .2, 0.15, color=black): |
| > | p:=plot([[-2,4],[2,4],[2,-4],[-2,-4],[-2,4]],-2.5..3.0,-4.5..5.0,scaling=constrained,axes=none, color=black): |
| > | pb:=plot([[[-2,2],[2,2]],[[-2,2.2],[2,2.2]]],color=black): |
| > | display(lz,lv,ll,s,p,pb); |
![[Maple Plot]](images/bjaelkeboejning12.gif)
| > | It:=int(b*z^2,z=-h/2..h/2); |
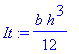
3. Taleksempel: E = 11 GPa , m = 10.0 kg , L = 2.0 m og b = 0.020 m .
| > | E:=1.1*10^10;m:=10.0;F:=m*9.82;L:=2.0;b:=0.02; |
![]()
![]()
![]()
![]()
![]()
Nedbøjningen for h = 0.02m
| > | h:=0.02; |
| > | It:=1/12*b*h^3; |
| > | 1/48*F*L^3/(E*It); |
![]()
![]()
![]()
Nedbøjningen for h = 0.03m
| > | h:=0.03; |
| > | It:=1/12*b*h^3; |
| > | 1/48*F*L^3/(E*It); |
![]()
![]()
![]()
Nedbøjningen for h = 0.04m
| > | h:=0.04; |
| > | It:=1/12*b*h^3; |
| > | 1/48*F*L^3/(E*It); |
![]()
![]()
![]()
| > |