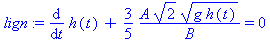
Gymnasieopgave : Tømning af beholder. Torricelli's lov 

> restart;with(plots):
 

Warning, the name changecoords has been redefined
 

***************************************************************************** 

Differentialligningen er 

lign:=diff(h(t),t)+6/10/B*A*sqrt(2*g*h(t))=0; 

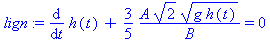
lign := (diff(h(t), t))+3/5*A*2^(1/2)*(g*h(t))^(1/2)/B = 0 

1. Den generelle løsning er: 

> los:=dsolve(lign,h(t));
 

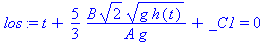
los := t+5/3*B*2^(1/2)*(g*h(t))^(1/2)/(A*g)+_C1 = 0 

Find h(t) 

> h:=solve(los,h(t));
 

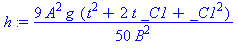
h := 9*A^2*g*(t^2+2*t*_C1+_C1^2)/(50*B^2) 

2. Den partikulære løsning h(0) = h0 . 

> s:=h0=subs(t=0,h);
 

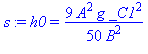
s := h0 = 9*A^2*g*_C1^2/(50*B^2) 

> C0:=solve(s,_C1);
 

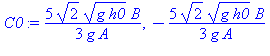
C0 := 5*2^(1/2)*(g*h0)^(1/2)*B/(3*g*A), -5*2^(1/2)*(g*h0)^(1/2)*B/(3*g*A) 

Den partikulære løsning bliver: 

> h:=expand(subs(_C1=C0[2],h));
 

h := 9*A^2*g*t^2/(50*B^2)-3*A*t*2^(1/2)*(g*h0)^(1/2)/(5*B)+h0 

Det kan skrives pænere 

> (h0^(1/2)-3/5*A/B*sqrt(2*g)*t)^2;
 

(h0^(1/2)-3*A*2^(1/2)*g^(1/2)*t/(5*B))^2 

> expand(%);
 

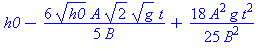
h0-6*h0^(1/2)*A*2^(1/2)*g^(1/2)*t/(5*B)+18*A^2*g*t^2/(25*B^2) 

3. Tømningstiden t0: 

> t0:=solve(h=0,t)[1];
 

t0 := 5*2^(1/2)*(g*h0)^(1/2)*B/(3*g*A) 

4. d1 = 0.4 m , d2 = 0.012 m og h0 = 0.70 m 

> g:=9.81;d1:=0.4;d2:=0.024;h0:=0.8;B:=evalf(Pi*d1^2/4);A:=evalf(Pi*d2^2/4);
 

g := 9.81 

d1 := .4 

d2 := 0.24e-1 

h0 := .8 

B := .1256637062 

A := 0.4523893422e-3 

Beholdervolumen V0 er ca 100 liter: 

> V0:=B*h0;
 

V0 := .1005309650 

5. t0 bliver ca 186 sekunder eller ca 3  minutter 

> evalf(t0);
 

> %/60.0;
 

186.9699175 

3.116165292 

Plot af h(t); 

> plot(h,t=0..186);
 

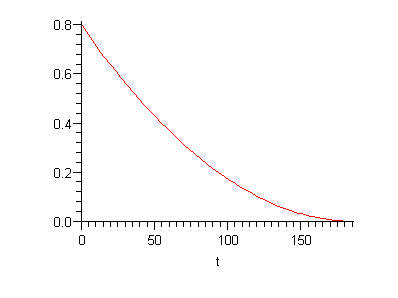
Plot 

>
 

>
 

>